赤外線の窓材は何が適切か？（３）

これまでの記事はこちらから
赤外線の窓材は何が適切か？（１）
赤外線の窓材は何が適切か？（２）

前回は第１回で列挙した「①光学的特性」のうち、”窓”としての機能を持たせる上で重要な「透過率」の観点から赤外線の窓材を検討した。今回はそれと同じく重要な「屈折率」の観点から窓材を議論したい。空気もしくは真空から窓材などの媒質に光がある角度\(\theta\)を持って入射する時、入射前後の媒質における光速の違いによって光線が曲がって見える現象が「屈折」であり、その入射前後の光速の比（光の進みにくさの指標）が屈折率である。窓材への入射角が0度であれば、入射前後で屈折は起こらない。そのため、なぜ屈折率が窓材の選択に影響を及ぼすのかがわからないという方もいるかもしれない（筆者の携わってきた分光器でも窓を0度入射の平行光線内に設置していたことしかなく、疑問に思っていた）。そこで媒質に入射する光のふるまいをもう少し細かに見ていこう。

例として、空気（屈折率\(n_1 = 1.0\)）から窓材（屈折率\(n_2\)）へと0度入射する光を考えよう。このときの入射光の強度を１とすると、一部の光は表面で反射され（R）、一部の光は窓材で吸収され（A）、残りが窓内を透過していく（T）。すなわち 1 = R + A + T という関係式が成り立つのだが、このいずれの量も屈折率（より正確には複素屈折率）が関係している。ここでの反射はフレネル反射と呼ばれることもあり、その原理については消えた波面の行方（ARコーティングとλ/4膜）その１および消えた波面の行方（ARコーティングとλ/4膜）その２に記載されているので、その記事を参照するとRは

$$R = \left|\frac{n_{1}-n_{2}}{n_{1}+n_{2}}\right|^2$$

で記述される。よく「ガラスは表面で4%の反射がある」という記述を見かけるが、これはこの式に空気の屈折率（\(n_1=1.0\)）と光学用に広く使用されているN-BK7などのフリントガラスの屈折率（\(n_1=1.5\)）を想定した場合のものであり、確かに

$$R = \left|\frac{1.0-1.5}{1.0+1.5}\right|^2 = (0.5/2.5)^2 = 0.04$$

であることがわかる。

残りの吸収・透過は複素屈折率が大きく関連する。複素屈折率（\(N\)）は光と窓材との相互作用（光の屈折・吸収）を同時に表すことのできる指標であり、以下の式で記述される。

$$N = n – i\kappa$$

複素屈折率の実部（\(n\)）はいわゆる屈折率そのものだが、虚部の\(\kappa\)は「消光係数」と呼ばれ、光が媒質内を伝搬する際に、単位長さあたりに媒質に吸収される割合を表している。一様な媒質内をx軸に沿ってすすむ光波の電場ベクトルは、振幅（\(E_{0}\)）、角振動数（\(\omega\)）、波数（\(k\)）、時間（\(t\)）を用いて

$$E(x,t) = E_{0}\exp{i(kx-\omega t)}$$

と表すことができる。ここで波数\(k\)は媒質内での波長\(\lambda\)を使用して \(k = \frac{2\pi}{\lambda}\) と表すことができるが、以前の記事「媒質中で変化するのは波長か？それとも振動数か？」で扱ったとおり、媒質内の波長は真空波長（\(\lambda_{0}\)）に対して\(\frac{1}{n}\)になるため、\(k = \frac{2\pi N}{\lambda_{0}}\)となる。ここに\(N = n – i\kappa\)を代入すると

$$E(x,t) = E_{0}\exp{i(\frac{2\pi n}{\lambda_{0}}x-\omega t)}\exp{\left(-\frac{2\pi \kappa}{\lambda_{0}}x\right)}$$

となる。\(\exp{\left(-\frac{2\pi \kappa}{\lambda_{0}}x\right)}\)は、\(x\)が増えるとともに小さくなるので、光の伝播とともに振幅が減衰することを示している（図１）。

 

　　

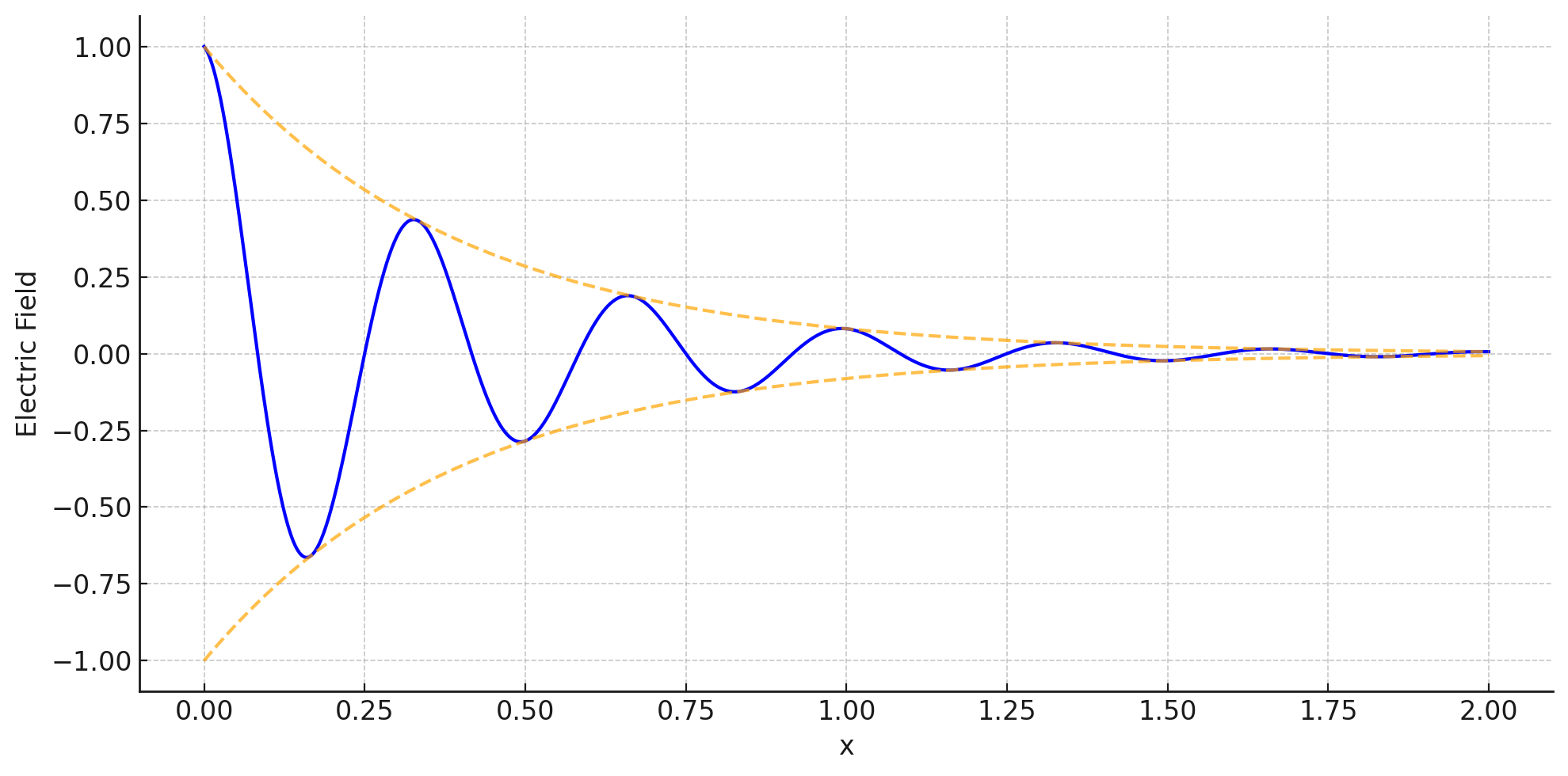
図１：吸収のある媒質内を伝搬する電場（の実部）。点線は\(\pm\exp(-\alpha x)\)を表す。

 

　　

さらに冒頭に出てきた吸収の強度Aは電場ベクトルの2乗に比例し、窓材の厚みを\(t\)とすると、\(A = |\frac{E}{E_0}|^2 \propto \exp{\left(-\frac{4\pi \kappa}{\lambda_{0}}x\right)}\)となる。この\(\frac{4\pi \kappa}{\lambda_{0}}\)は吸収係数（\(\alpha\)、attenuation coefficients）と呼ばれ、単位長さ（1cm）あたりの吸収量に相当する量である。余談ではあるが、弊社のスタッフの１人は、「赤外線用イマージョングレーティング」に用いるための、光学材料の吸収係数を高精度に求めるための実験系および測定システムの構築に携わっていた。天文学用途のように超高感度の装置が要求される場合は光学素子を低温にする必要があり、その環境における吸収係数の値が必要である。また、わずかな吸収でも問題となるので、その精度も重要である。しかしながらそのような測定結果はほとんど公表されていなかったため、測定装置の開発から始めざるを得なかった。機会があればその測定の紹介もできればと思う。

ここまで紹介した反射・吸収が小さいほど光が透過するため、透過にも屈折率が関わっていることになる。様々な波長、材質での屈折率はいくつかのまとめページが存在しており、たとえはこのページでは様々な材料がラインナップされている。選定の際には、装置の設置環境や波長域などの条件からARコーティングを施すことができない場合は、フレネル反射を抑えるためにより屈折率の低い材料が良い。反対に収斂（発散）光束中に置かれる場合において、その集光点をできるだけ光学装置の内部に設定したいという要求がある場合は屈折率の高い材料が望ましいこともある。