媒質中で変化するのは波長か？それとも振動数か？

真空中を進む波の振動数\(f\)と波長は、真空中の光速\(c\)を使って、\(f=\frac{c}{\lambda}\)という関係式によって結び付けられる。屈折率\(n\)の媒質中における光速は屈折率の定義から\(v=\frac{c}{n}\)であるため、媒質中での振動数\(f’\)は

$$ f’ = \frac{v}{\lambda’} = \frac{c}{n\lambda’}\tag{1} $$

となる。ここで、媒質中の波長が\(\lambda’=\frac{\lambda}{n}\)の関係式を満たすと仮定すると、\(f=f’\)となって媒質中であっても振動数が維持される（「振動数不変則」が成り立つ）ことが導かれる。しかしながらちょっと待ってほしい。\(f’=nf\)と仮定した場合はどうなのか？その場合であっても、\(\lambda’=\lambda\)とすれば振動数と波長の関係も屈折率の定義とも矛盾のない結果が得られ、「媒質中では振動数でなく、波長が不変」という結論になる。教科書に書いてある「振動数の方が不変」という根拠はどこにあるのか？今回はこの点について考えてみたい。

この問いに対する答えは電磁気学の教科書に見つけることができる。しかしながら多くの教科書では厳密性・一般性を失わないようにするために、３次元空間を伝搬する電磁波についてこの議論を展開しており、初学者にとっては非常に難解な議論になってしまっている。そこで、本稿ではできるだけ本質のみを抽出するべく、できるだけシンプルなモデル（図１）で考えてみることにする。ここでは屈折率\(n_{i}\)と屈折率\(n_{t}\)の媒質が平面の境界面をもって仕切られており、屈折率\(n_{i}\)の媒質から屈折率\(n_{t}\)の媒質に向かって（x軸に沿って）、垂直に光線が入射している状況を考える。界面では、透過光線と反射光線が生じる。

 

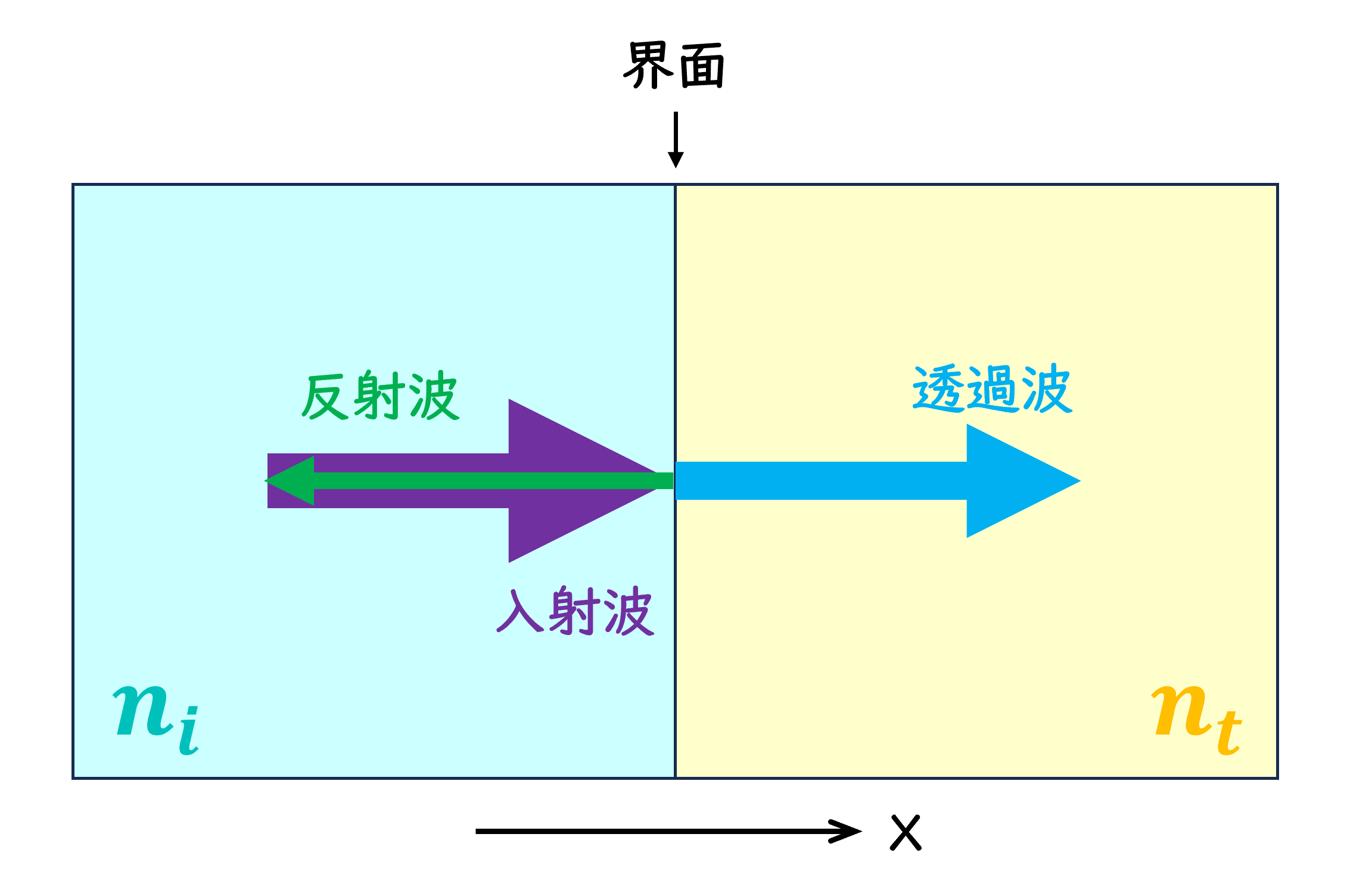
図１：境界面を境に屈折率が異なる媒質（\(n_{i}\)と\(n_{t}\)）にx軸に沿って入射する光線の模式図。界面では透過光線と反射光線が生じる。

 

入射光線、透過光線、反射光線を波面として取り扱ったとき、それぞれの振幅を、\(E^{0}_{入射}\)・\(E^{0}_{透過}\)・\(E^{0}_{反射}\)、振動数を\(f_{入射}\)・\(f_{透過}\)・\(f_{反射}\)、速度を\(v_{入射}\)・\(v_{透過}\)・\(v_{反射}\)とすると、ある時刻\(t\)、位置\(x\)における波面（電場）は以下のよう表現される。

$$ E^{0}_{入射}(x,t) = E^{0}_{入射}\sin\left[2\pi f_{入射}\left(t-\frac{x}{v_{入射}}\right)\right]\tag{2} $$
$$ E^{0}_{透過}(x,t) = E^{0}_{透過}\sin\left[2\pi f_{透過}\left(t-\frac{x}{v_{透過}}\right)\right]\tag{3} $$
$$ E^{0}_{反射}(x,t) = E^{0}_{反射}\sin\left[2\pi f_{反射}\left(t-\frac{x}{v_{反射}}\right)\right]\tag{4} $$

ここで界面のx座標を\(x=0\)とすると、界面においては界面に平行な電場成分が保存されるため、

$$ E^{0}_{入射}(0,t) + E^{0}_{反射}(0,t) = E^{0}_{透過}(0,t)\tag{5}$$

が満たされる（要は、媒質i側の電場と媒質t側の電場が等しくなる）。式（２）～（４）を式（５）に代入すると、

$$ E^{0}_{入射}\sin[2\pi f_{入射}t] + E^{0}_{反射}\sin[2\pi f_{反射}t] = E^{0}_{透過}\sin[2\pi f_{透過}t]\tag{6}$$

が得られる。この式は３つの正弦波から成っており、透過波面が入射波面と反射波面の足し合わせとなっていることがわかる。また、任意の時刻、つまり常に成り立っていなければならない。その様子を示したのが図２と図３である。

 

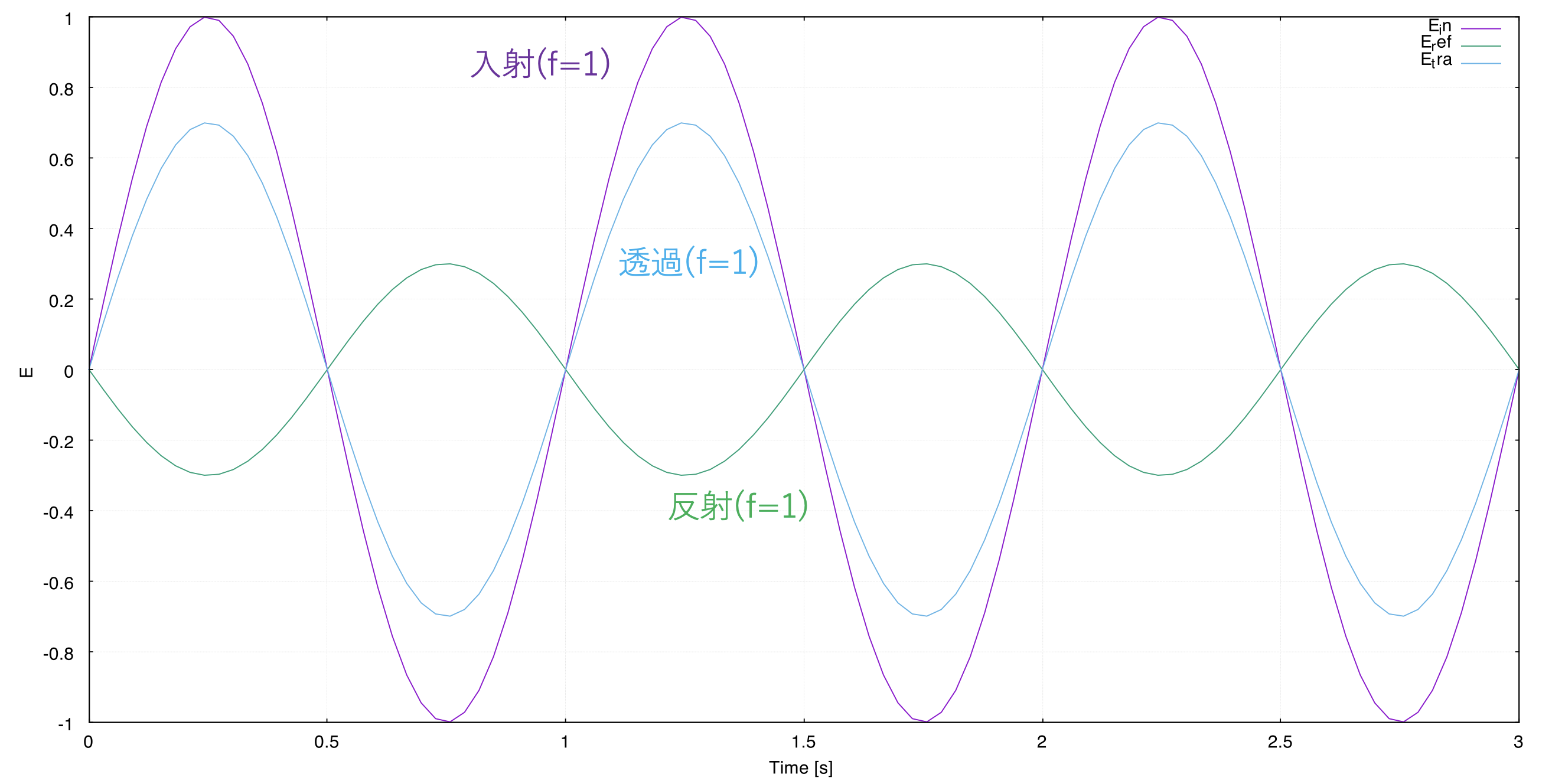
図２：入射波面、透過波面、反射波面の電場（E）の様子（\(E^{0}_{入射}=1.0\)、\(E^{0}_{反射}=0.3\)、\(f_{入射}=f_{反射}=1[Hz]\)のとき）

 

 

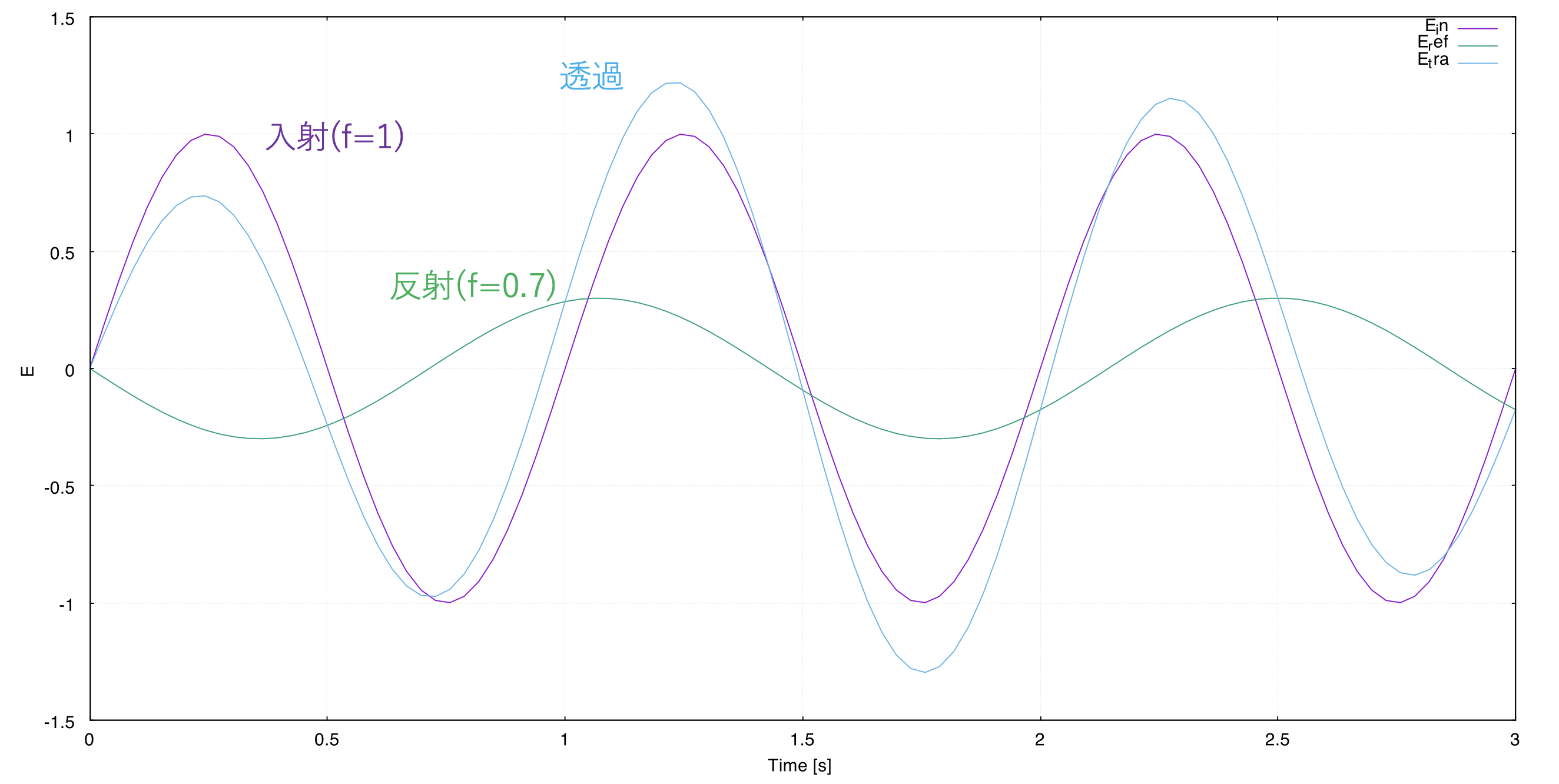
図３：入射波面、透過波面、反射波面の電場（E）の様子（振幅は図２と同様で、振動数が\(f_{入射}=1[Hz]\)、\(f_{反射}=0.7[Hz]\)のとき）

 

図２では\(E^{0}_{入射}=1.0\)、\(E^{0}_{反射}=0.3\)、\(f_{入射}=f_{反射}=1[Hz]\)とし、それぞれを紫色、緑色で示してある。この場合、定式によって透過波の時間変化の様子が決まるが、それは水色で示されている。図から明らかに、\(f_{透過}=1[Hz]（=f_{入射}=f_{反射}\)であることがわかる。一方で、図３は入射波と反射波の振幅を維持したまま、振動数を\(f_{入射}=1[Hz]\)、\(f_{反射}=0.7[Hz]\)としたものである。得られた反射波の振幅（最大値と最小値）は波が振動する度に変化しており、もはや一つの正弦波として書けていないことがわかる。ここでは一例のみしか挙げていないが、反射波（もしくは透過波）の振動数が入射波と異なると、どんな場合であっても透過波（もしくは反射波）が１つ振動数を持つ正弦波で表現することはできない（＝つまり、波として存在できない）。よって、式（５）を満たせるのは、周波数において\(f_{透過}=f_{入射}=f_{反射}\)の場合のみであり、これによって振動数不変の法則が示されたことになる。なお、３つの波の振動数が不変であることはフーリエ変換を理解されている人であればもっと理解しやすいかもしれない。媒質\(i\)での合成波が２つの振動数の成分を持つならば、媒質\(t\)中の波は２つの振動数の成分を持たなければならず、透過波は一つの正弦波という仮定と矛盾してしまう。

結局のところ、「界面においても入射波、透過波、反射光が時間によらず定常」、ということが３つの波の振動数を一定にならしめていることになる。振動数が一定である一方で、異なる媒質中では波の位相速度が異なることによって生じるおつりは、波の基本式に現れる残りの変数である波長に押し付けざるを得ない（式（１））。これが、媒質中で波長が\(\frac{1}{n}\)になり、振動数は変化しない理由である。