赤外線の窓材は何が適切か？（４）

これまでの記事はこちらから：
赤外線の窓材は何が適切か？（１）
赤外線の窓材は何が適切か？（２）
赤外線の窓材は何が適切か？（３）

今回から、第１回で列挙した「②機械的特性」を取り扱う。窓を含む光学系の設計は一般的には「①光学的特性」に基づき、どのようなレンズ・ミラーの組み合わせが良いかを探索する。しかしこれら光学素子は空に浮いているわけではなく、何らかの機構によって保持をする必要がある。「Optmecanics（オプトメカニクス）」という言葉があることからもわかるように、光学系を設計するときには機械系の観点からも注意すべき点がいくつかあるのだ。そして光学材料は金属のように延性・展性があるわけではないため、許容以上の荷重がかかると伸縮することなく破損する。またその破損個所は必ずしも荷重がかかった点とは限らないことも注意が必要である。今回は機械的特性のうち破損の観点で重要な剛性（ヤング率）について解説する。

円柱状のものがあったときに、その両端を引っ張るとその円柱が伸び、やがて破断する。このとき物体には引っ張る力に対してもとに戻ろうとする力が発生し、この力を応力（stress、\(\sigma\)）という。応力の大きさは引っ張る力と同じであり、単位面積あたりの力\([N/m^2]\)で表す。また元の長さに対する伸び量のことをひずみ（strain、\(\epsilon\)）と言う。この応力とひずみの関係を示したのが図１である。金属のように延性のある材料は応力に応じてひずみが緩やかに増加してゆき、ある程度のところで破断するのに対し、セラミックスをはじめとする光学素子に用いられる脆性材は伸び量が小さく、曲線の傾きが大きいという特徴がある。この傾きのことをヤング率（Young’s modulus、\(E\)）といい、以下の式で表される。

$$ E = \frac{\sigma}{\epsilon} $$

 

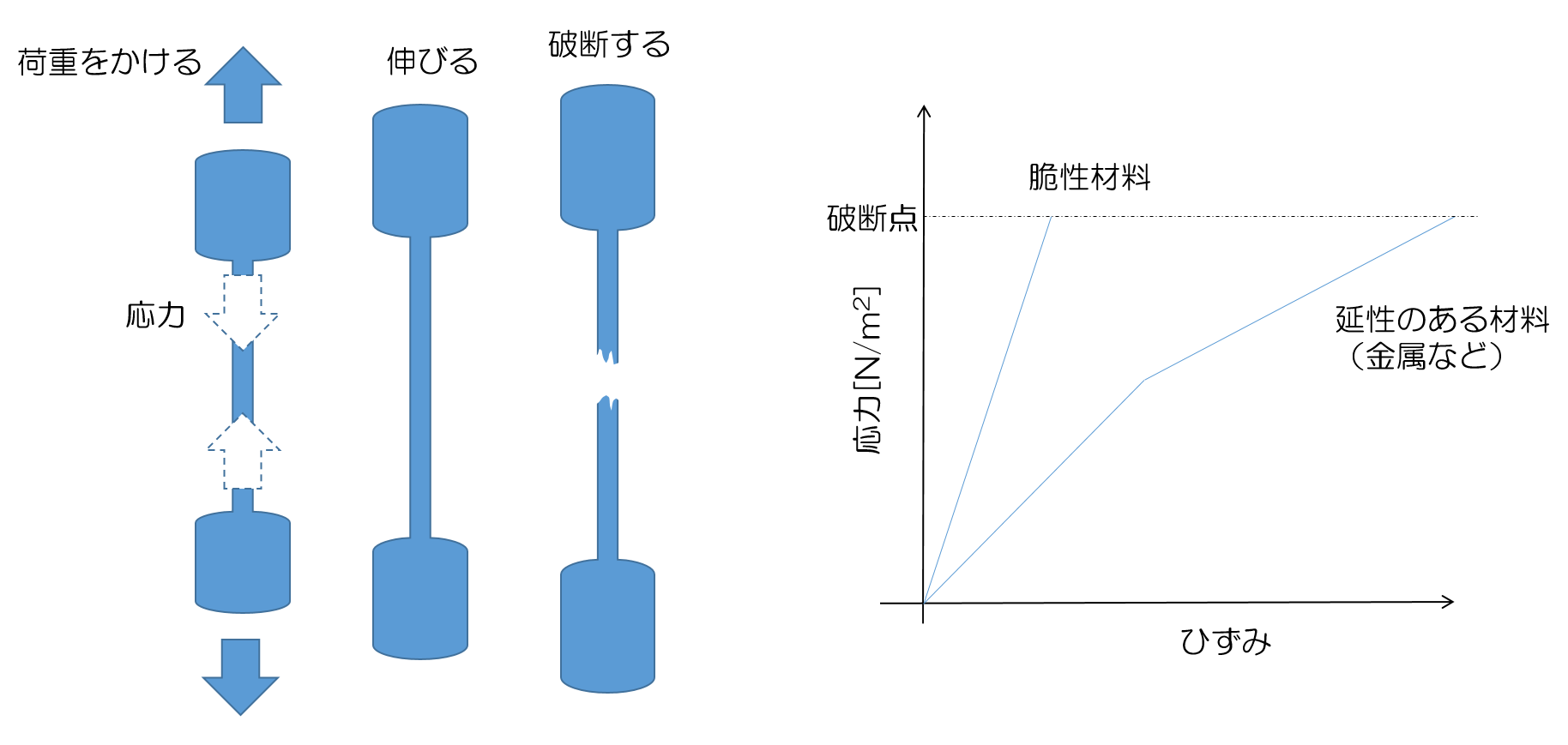
図１：応力-ひずみ曲線の模式図

 

ヤング率を求めるには図１にある応力-ひずみ曲線を描くため、引張試験を実施するのだが脆性材はこの試験に不向きである。というのも、一般的な物質では引張試験片に図１の左のような形状のサンプルを用い、破断も円柱中央部の細い箇所で起こるのだが、脆性材は中央部以外のところでも破断が起こるため、測定がうまくできない。実際には３点曲げ試験・４点曲げ試験を行いヤング率を測定する（今回は曲げ試験については深く解説せず、また別の機会に譲ることにしよう）。
なお脆性材は破断に至るまでであれば、応力（引っ張る力）を0にすることで、まるでばねのような弾性体のように元の形状に戻る。またこのように両端を引っ張ると、形状が図２のように変化する。この形状の断面側・長さ側の伸び量の比のことをポアソン比（Poisson’s ratio、\(v\)）と言い、以下の式で表される。

$$ v = \frac{\frac{\Delta d}{d}}{\frac{\Delta l}{l}} $$

 

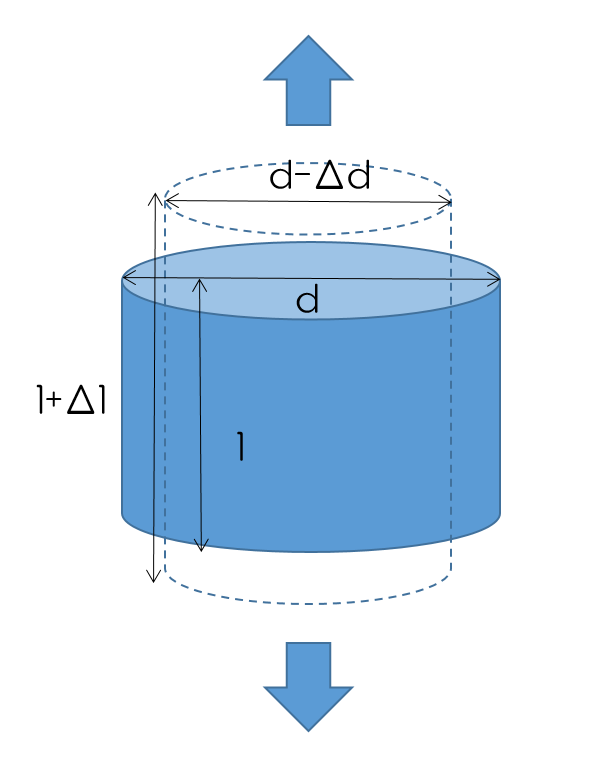
図２：引っ張りによる形状変形の模式図

 

光学材料に用いられるセラミックス材のポアソン比は0.2～0.3程度、もう少し粘度の高いプラスチック材のポアソン比は～0.5程度になる。

しかし窓材を考慮するうえでは、変形はすることがある可能性があるためポアソン比を求めることは重要そうな気がするが、なぜヤング率が必要なのだろう？と思われる読者もいるかもしれない。実はヤング率とポアソン比はそのほかの機械的性質に関係があり、たとえば体積弾性率（Bulk Modulus、\(k\)）やせん断弾性率（Shear Modulus、\(\mu\)）（図３）はこれらを用いて記述することができる。

$$ k = \frac{P}{\frac{\Delta V}{V}} = \frac{E}{3-6v} $$
$$ \mu = \frac{\frac{\Delta d}{d}}{\frac{\Delta l}{l}} = \frac{E}{2+2v} $$

 

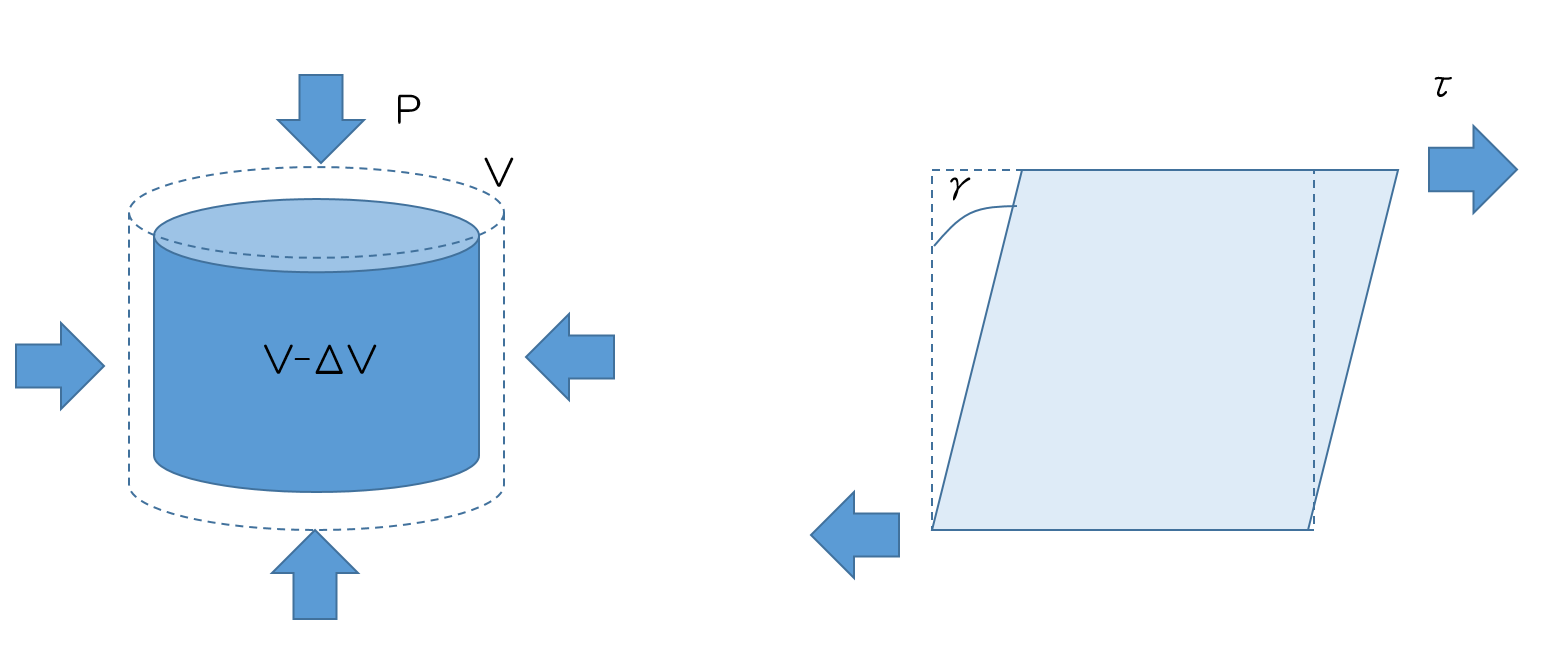
図３：一様な圧縮による変形（左）とせん断変形（右）の模式図

 

脆性材のポアソン比は約0.2～0.3程度なので、体積弾性率はヤング率の約0.55倍、せん断弾性率はヤング率の約0.4倍になる。もちろん剛性を示す指標としても重要だが、その他の機械的性質の評価の基準とすることもできるため、これらの値を押さえておくことは重要なのだ。次回は窓材の破壊と圧力の関係についてまとめたいと思う。