
天体写真や観測において、「ノイズ」と「S/N(SN比)」は実に様々な場面で出くわす言葉だろう。だが一方で(あくまで著者の経験レベルだが)これらの言葉はよく混同されがちで、区別をせずに同一のものとして使われている場面に良く遭遇する。今回はこれらの言葉の正しい定義と違いを解説しよう。
いま、望遠鏡で集められた天体光がカメラの検出器(CCDやCMOS)に入射し,あるピクセルに電子が溜まった状態を考えよう。注目するピクセルの出力値に含まれるのは、天体の真の値、系統誤差、ノイズであり、そのイメージは図1のようになるだろう。なお図1の直方体の高さがそれぞれのカウント値を表す。
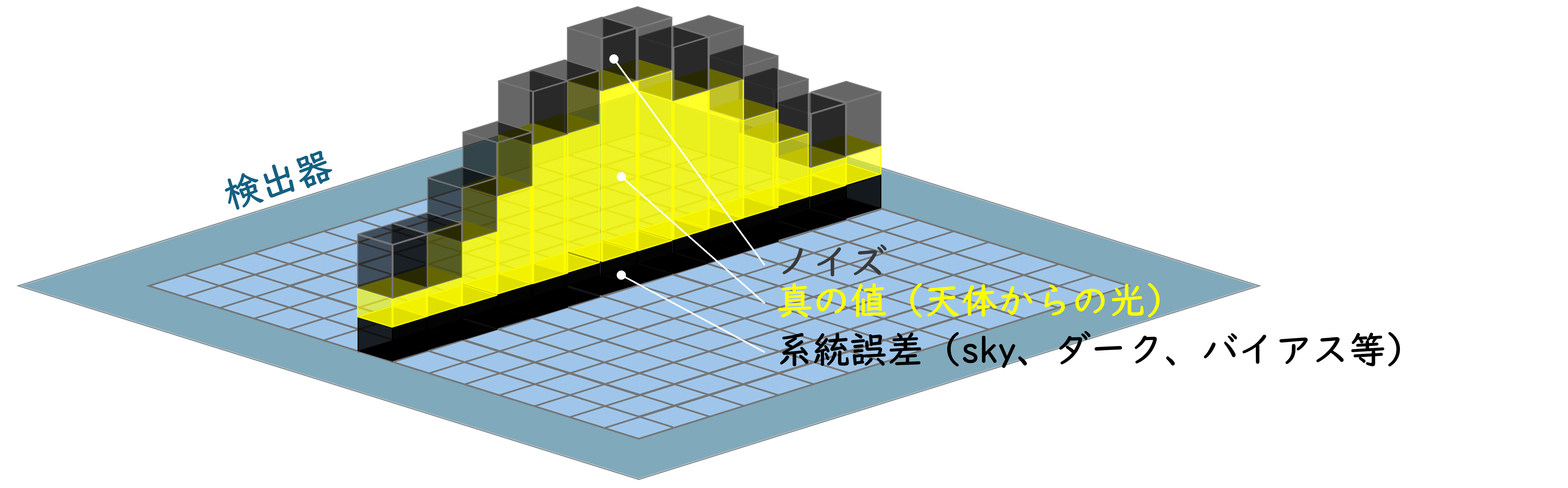
図1:電子の溜まったピクセルのカウントに含まれる真の値、系統誤差、ノイズのイメージ
この図の中で
シグナル(S)=「真の値」
N ≒「ノイズ」
である。なお、「ノイズ」はあくまでも ≒ Nである。より正確な定義は別の記事にて解説予定。)
ノイズとは、ピクセルの出力値に含まれるすべての偶然誤差のことである(天体写真における「ノイズ」の正体 その1と
天体写真における「ノイズ」の正体 その2で詳しく解説した)。これにはダークノイズ、背景光ノイズ、天体光のフォトンノイズ、リードアウトノイズ等が含まれる。
「S/N」とは記号が表しているとおり、天体の真の値(S)とノイズ(N)との大きさの比のことで、割り算S\(\div\)Nで求められる。一般に真の値Sが大きくなれば、ノイズNもその分大きくなるのだが、大抵の場合Sに比べてNの増加率が鈍いため、真の値Sが大きくなればなるほどS/Nも大きく(良く)なっていく。つまり画像を重ね合わせる「コンポジット処理」により合計露出時間を増やすと、シグナルSが大きくなるのでS/Nも大きく(良く)なるのだ。
このように、「ノイズ」と「S/N(SN比)」は異なるものである。天体写真の撮影において、露出時間を増やすと、天体光のフォトンノイズなどのために、実はノイズも増えているのだが、それ以上に天体からの光によってシグナルが増えるため、結果としてS/Nが大きくなる。
また、たまに聞く話として「加算平均コンポジットの場合は、コンポジット後のSは大きくならないので、S/Nが向上しない」というものがあるが、これは間違いである。コンポジット前の1枚画像のシグナルを\(S_{0}\)、ノイズを\(\sigma_{0}\)として、n枚の画像を加算した場合、シグナルは\(nS_{0}\)、ノイズは \( \sqrt{n}\sigma_{0}\)となる(ノイズは\(n\sigma_{0}\)とならないことに注意)。一方、加算平均の場合は、加算後に更に画像枚数nで割るため、シグナルは\(S_{0}\)、ノイズは\( \frac{\sigma_{0}}{\sqrt{n}}\)となる。つまり、加算でも加算平均でも、コンポジット後のS/Nは\( \sqrt{n}\frac{S_{0}}{\sigma_{0}}\)で同じなのだ。
(注意:ただしこれが成り立つのは画像処理ソフト内部の計算において十分大きな階調空間を使える場合で、例えばStellaImage等で使うFitsファイルには十分大きな階調空間があるために、加算でも加算平均でもS/Nは変わらない)
天体写真撮影では非常に淡い天体を撮影するため、一般にSが小さくS/Nが悪くなりがちだが、コンポジット処理を行い合計の露出時間を長くすることでS/Nを向上させ、シグナルに対して相対的にノイズを小さくし、天体写真の見栄えを向上させている。

大学院在学中は素粒子物理学を専攻。趣味の天体写真も物理理論に裏付けられた解析方法を行っており、 アマチュア天文家の間で蔓延している都市伝説は一切信じない。赤道儀マニアでアマチュア天文機器にやたら詳しい。 計算機ホログラム(CGH)や干渉計などの高度な物理計算を軽々とこなす。 光学・物理学に関連する原理や数学的理解に関する記事を担当。