ノイズを計算する（２）

天体写真の画像処理の過程では、ダーク減算、フラット補正、コンポジット等、画像に対して様々な「演算」を行う。具体的には、各処理において画像内の各ピクセルのカウント値に対して以下の操作を行っている。

ダーク減算　→　引き算
フラット補正　→　割り算
コンポジット　→　足し算（or平均）

各CCD/CMOSのピクセルに載っているノイズはこれらの演算操作の元でどうなるだろうか？

「ノイズが各種演算でどのように移り変わっていくか」というのは数理統計の分野では「誤差の伝播」と呼ばれ、結論から言うと誤差の伝播を計算する公式が存在する。いま、\(A,B,C,･･･\)の測定値から計算の結果\(U\)の値が求まる場合を考える。このことを関数\(F\)を用いて数式で書くと、\(U=F(A,B,C,\cdots)\)となる。このとき\(A,B,C,･･･\)のそれぞれの測定値が標準偏差\(\sigma_A、\sigma_B、\sigma_C\)を持っているとき、計算結果の\(U\)の標準偏差\(\sigma_U\)は以下で求まる：

\begin{align*} \sigma_U = \sqrt{\left( \frac{\partial F}{\partial A}\right)^2 \sigma_A ^2 + \left( \frac{\partial F}{\partial B}\right)^2 \sigma_B　^2 + \left( \frac{\partial F}{\partial C}\right)^2 \sigma_C ^2 + \cdots} \tag{1}\end{align*}

（注：これは変数A、B、C、･･･間には相関が無い場合の公式だが、天体写真に関する場合ほとんどの状況でこの式で十分である。）

（１）式には偏微分等があって少し難しいのと、いきなり天体写真の場合について考えると難しいので、最初は定規を使って図１の円柱の体積を求める例を考えよう。

 

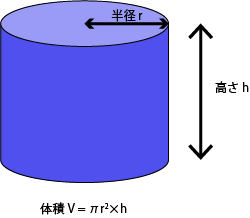
図１：円柱の例

 

定規を使ってこの円柱の半径\(r\)と高さ\(h\)を測ったところ、それぞれ

\begin{align*} r &= 5.0 \pm 0.2 \text{[cm]}\\ h &= 8.0 \pm 0.1 \text{[cm]} \tag{2}\end{align*}

だったとしよう。ここで\(\pm 0.2\)と\(\pm 0.1\)はそれぞれ\(r\)と\(h\)の測定時の偶然誤差（ノイズ）の標準偏差である。円柱の体積は\(V=\pi r^2 \times h\)で求まるので、測定の偶然誤差を気にしなければ

\begin{align*} V &= \pi r^2 \times h\\ &= 3.14\times(5.0)^2\times8.0\\ &=682 \text{cm}^2 \tag{3}\end{align*}

と求められる。しかし測定値\(r\)と\(h\)はそれぞれ誤差を含んでいるので、それらを使って計算された体積\(V\)にも誤差が含まれているはずだ。その誤差の標準偏差を求めるのに誤差の伝播公式（（１）式）を使う。ここでは半径\(r\)、高さ\(h\)から体積\(V\)を求めることを考えているので、誤差の伝播公式中の文字は\(U=V，A=r，B=h\)となり、\(C\)以降がない形になる。公式中の関数\(U=F(A,B,C,\cdots)\)はここでは\(V=F(r,h)=\pi r^2 \times h\)である。これを誤差の伝搬公式に代入すれば、

\begin{align*} \sigma_V &= \sqrt{\left(\frac{\partial V}{\partial r}\right)^2 \sigma_r ^2 + \left(\frac{\partial V}{\partial h}\right)^2 \sigma_h ^2}\\ &=\sqrt{(2 \pi r h)^2 \sigma_r ^2 + (\pi r^2) \sigma_h ^2}\\ &=\sqrt{(2\times3.14\times5.0\times8.0)^2 \times (0.2)^2 + (3.14\times (5.0)^2)^2 \times (0.1)^2 }\\ &\unicode{x2252}50.8 \text{cm}^2 \tag{4}\end{align*}

と体積\(V\)に含まれる誤差を求めることが出来る。従って体積\(V\)を誤差を含めて記述することができる(最後の式変形では有効数字を考慮して四捨五入を行っている)。

\begin{align*} V &\unicode{x2252} 682.0 \pm 50.8\\ &\unicode{x2252} 680 \pm 50 [\text{cm}^2] \tag{5}\end{align*}