
以前の記事で、多層膜によってレンズやフィルター面でのフレネル反射を抑制するためのARコーティングの原理について紹介した。その時に主役となったのは、「λ/4膜」という光路長が丁度λ/4の厚さになる薄膜であった。実はこのλ/4膜、ガラス面に積層することで反射率を増加させ、多層膜から形成される「ミラー」を構成することも可能なのである。ARコーティングが透過率を100%に近づける膜であったことを考えると、これは全く逆の効果。なんとも不思議な話に聞こえるが、今回はその秘密について解説したい。
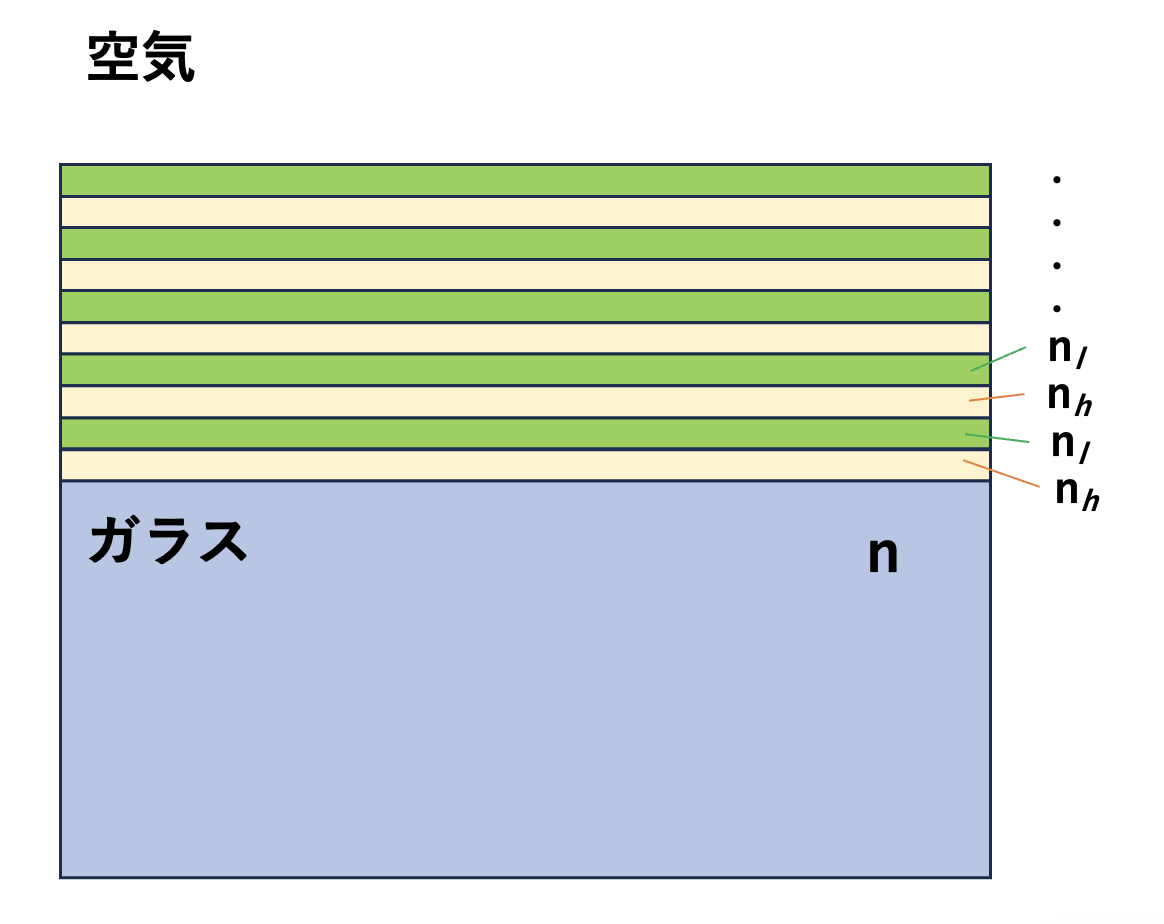
多層膜によるミラーを実現するには、2種類の材料からなるλ/4膜を用いる。この2種の材料の屈折率をそれぞれ、\(n_{h}\)と\(n_{l}\)(ただし、\(n_{h} > n_{l}\))とする。これらの2種の材料からなるλ/4膜を、図1のようにガラス(屈折率n)に積層することを考える。膜に入射した光波は、空気と\(n_{h}\)膜の界面、\(n_{h}\)膜と\(n_{l}\)膜の界面、\(n_{l}\)膜とガラスとの界面から反射されて、空気側に戻ってくるが、その際に発生する光路差をそれぞれ\(\Delta L_{1}\)、\(\Delta L_{2}\)、\(\Delta L_{3}\)とすると
$$\Delta L_{1} = \frac{\lambda}{2}$$
$$\Delta L_{2} = \frac{\lambda}{4} \times 2 = \frac{\lambda}{2}$$
$$\Delta L_{3} = \left(\frac{\lambda}{4} \times 2\right) + \left(\frac{\lambda}{4} \times 2\right) + \frac{\lambda}{2} = 3\frac{\lambda}{2}$$
となり、すべての位相が波長の整数倍で揃うことが分かる。
(\\Delta L_{3}\)の計算の第3項に現れているλ/2は、固定端反射に伴って発生する位相差である。その原理については反射光における位相のジャンプ:固定端と自由端(1)および反射光における位相のジャンプ:固定端と自由端(2)を参照されたい)。
このことは、すべての反射光は強め合い、反射光が増幅することを意味する。

図1の構成によって確かに反射率が増加することが確認できたが、それぞれの界面での反射率はせいぜい数%なので、それらが重ね合わさってもミラーと呼べるような大きな反射率は達成できない。そこで、この\(n_{h}\)膜と\(n_{l}\)膜のペアを無数に重ねていくことを考える(図2)。この場合、膜の数に応じた反射光が発生するので、それに応じた無数の波面の重ね合わせた合成波面が発生することになる。塵も積もれば…によって、それら個々の重ね合わせた波面エネルギーのは100%にかぎりなく近づいていき、その結果多層膜はミラーとして用いることが可能になる。
なんともあっけないが、これが多層膜ミラーの基本原理である。しかしながら、またここである疑問が発生する。「基準波長λ以外ではミラーとして機能するのか?」という疑念である。基準波長λ以外の波長(例えば波長λ+Δλ)においては、各層から発生した反射波面間の位相は明らかにずれており、完全な強め合いが発生することはない(むしろ積極的に弱め合うこともありえる)。とすると、ミラーとしては単一波長(基準波長)でのみしか用いることができず、レーザーアプリケーションを除く光学用途としてはほとんど無用の長物となってしまうように思える。しかし、安心してほしい。結果はそこまで悲観的なものでなく、(金属ミラーのように広い帯域は持たないものの)ある程度の波長範囲においては高い反射率を示すのである。次回はその理由について、ARコーティングの多層膜化の効用 その1で解説したベクトル図法を用いた定性的な説明を展開する。

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。