金属が反射する理由（わけ）：その２

プラズマ振動数\(\nu_{p}\)は、電子の空間密度を\(N\)、素電荷を\(e\)、自由電子の有効質量を\(m\)、真空の誘電率を\(\varepsilon_{0}\)とすると、

$$ \nu_{p} = \frac{1}{2\pi}\sqrt{\frac{N}{m \varepsilon_{0}}}e$$

と表すことができる。この式から、電子の密度が高いほどプラズマ周波数は大きくなることが分かる。前回の記事で述べたように、プラズマ振動数より低い振動数をもつ電磁波は、金属内部に進入することができずに表面で反射する。表１に、上式を用いて金、銀、銅、アルミニウムについてプラズマ振動数を計算した結果を示す。ここで、電子密度は原子量と密度および価電子から推定した値である。また電子の有効質量は、電子の静止質量としてある。よって、若干の誤差を含んでいる可能性があることはご了承いただいきたい。

 

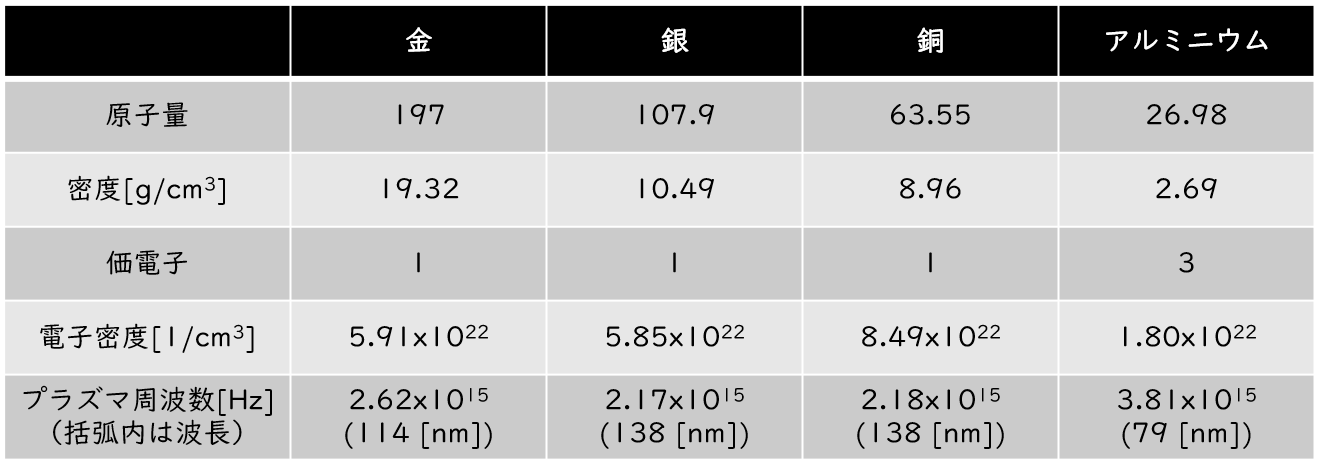
表１：各種金属のプラズマ振動数

 

表を見ると、ここで挙げたすべての金属プラズマ振動数は紫外線領域にあり、よって紫外線より長い可視光や赤外線波長において十分に高い反射率を示すことが分かる。つまり、これらの金属が可視光で高い反射率を維持することと矛盾がない。ただ待ってほしい。実際の金属ミラーの反射率に詳しい方はすぐさまこの計算結果が変であることに気づくだろう。「紫外線～電波領域まで広い波長領域で高い反射率を示すアルミニウムはここでの計算結果と実験と一致しているようだが、金や銀、銅は実際には紫外線を反射しない。計算もしくは理論がおかしいのではないか？」と。そのご指摘はもっともで、この実験と計算結果の不一致は別の物理過程を考慮することで解消される。その内容については次回に譲る。

その代わり、定性的な説明では満足できない方のために、プラズマ振動数について少しだけ補足をしておく。プラズマ内の自由電子のふるまいは、自由電子に対する運動方程式（以下）を解くことで得られる。

$$ m\frac{d^2x}{dt^2} = eE(t) – \gamma \frac{dx}{dt}$$

ここで、\(x\)は電子の位置、\(E(t)\)は外部電場の時間変化、\(\gamma\)は運動する電子に働く摩擦係数である。上式より電子が振動する振幅（\(x_{0}\)）を導出し、分極（\(=- N_{e}x_{0}\)）から比誘電率\(\varepsilon_{r}\)を導出することができる（ここで得られた解は”Drudeの式”と呼ばれる）。\(\varepsilon_{r}\)は一般には複素数になるが、実部が0になるときの振動数がプラズマ振動数である。もう少し簡単には、+の電荷と－の電荷が混じっている気体（いわゆるプラズマ）を考え（図１）、＋の気体（もしくは－の気体）だけを一方向に\(x_{0}\)だけずらしたときに、電気的な復元力によって振動が発生する振動数を求めることによっても同じ式を得ることができる。後者を導出する際の前提条件から分かるように、プラズマ振動数とは、実はプラズマの密度ゆらぎの固有振動数であり、いわゆる音波である。たまにプラズマ振動数として「プラズマが持つ”電磁波の”固有振動数の一つ」といった説明を見かけることがあるが、これは大きな誤解であることを強調しておきたい。

 

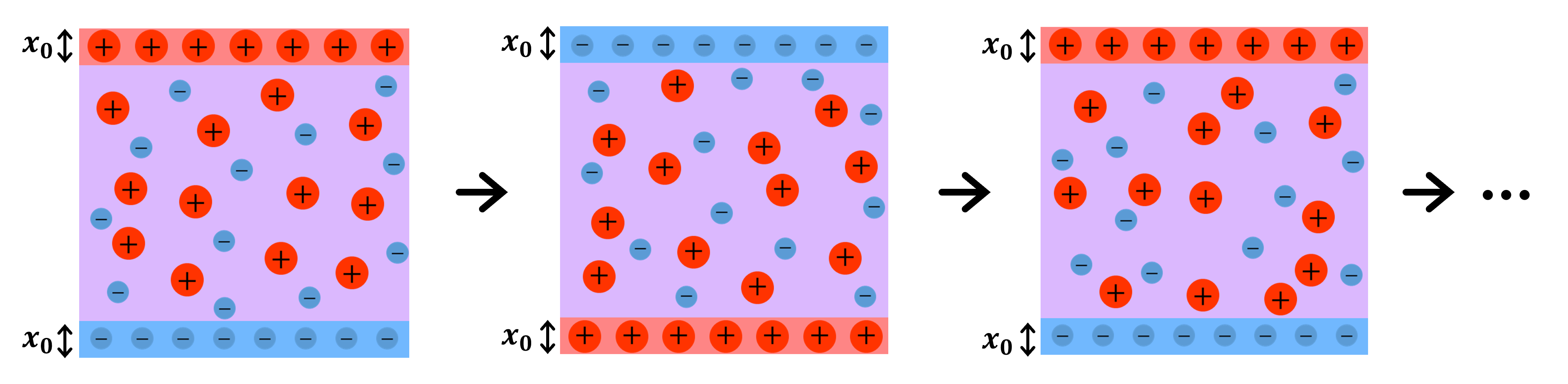
図１：プラズマ振動数の概念図

 

では、本来関連のない音波であるプラズマ振動数が電磁波と、どう関係しているのだろうか？この点についても、紙面が許せば次回以降に解説したい。