ノイズを計算する（３）

「ノイズ」と「S/N（SN比）」の違いでも紹介したとおり、CCD/CMOSの各ピクセルのカウント値にはノイズが含まれる。簡単のため系統誤差は既に十分取り除かれているものとすると、残るはカメラの性能とは無関係なノイズ（偶然誤差）であり、こちらは原理的に取り除けないものであった。

 

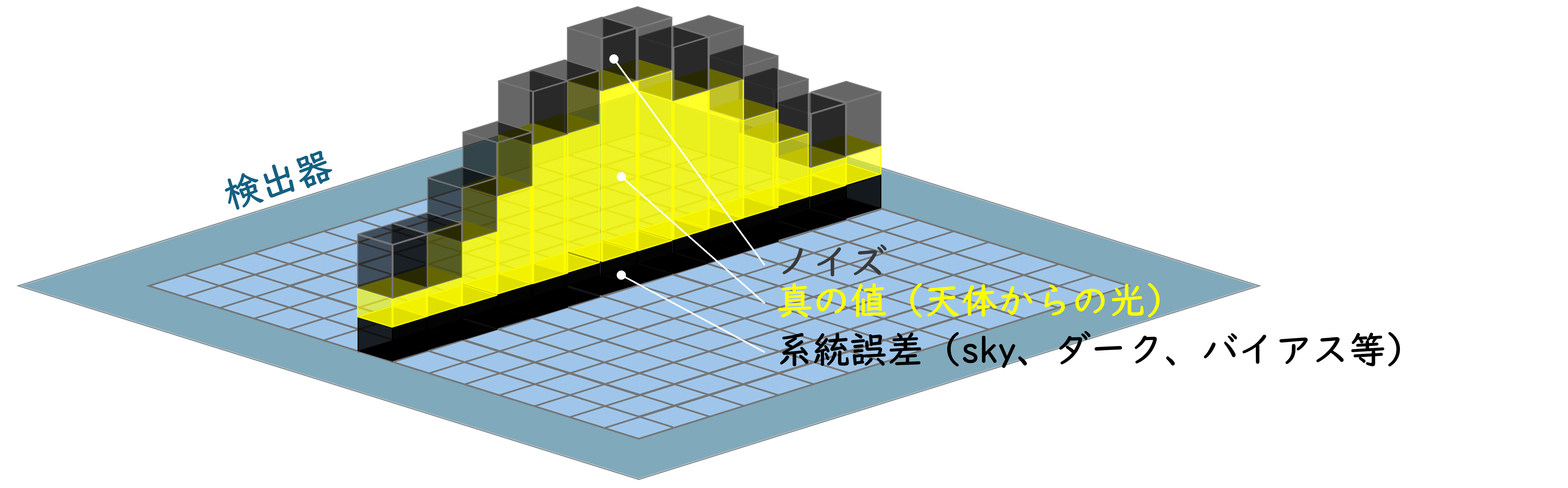
図１：電子の溜まったピクセルのカウントに含まれる真の値、系統誤差、ノイズのイメージ

 

天体写真ではコンポジットによって各フレームの対応するピクセル同士を加算（加算コンポジット）もしくは平均を取る（加算平均コンポジット）という操作をしている。天体写真のノイズに関して実際に誤差の伝播の式を使ってコンポジットがどう影響を与えるのかを見る前に、誤差の伝播の式をもう一度書いておこう。

\(A,B,C,･･･\)の測定値から計算の結果\(U\)の値が求まる場合を考える。このことを関数\(F\)を用いて数式で書くと、\(U=F(A,B,C,\cdots)\)となる。このとき\(A,B,C,･･･\)のそれぞれの測定値が標準偏差\(\sigma_A、\sigma_B、\sigma_C\)を持っているとき、計算結果の\(U\)の標準偏差\(\sigma_U\)は以下で求まる： \begin{align*} \sigma_U = \sqrt{\left( \frac{\partial F}{\partial A}\right)^2 \sigma_A ^2 + \left( \frac{\partial F}{\partial B}\right)^2 \sigma_B　^2 + \left( \frac{\partial F}{\partial C}\right)^2 \sigma_C ^2 + \cdots} \tag{1}\end{align*} （注：これは変数A、B、C、･･･間には相関が無い場合の公式だが、天体写真に関する場合ほとんどの状況でこの式で十分である。）

まずはN枚の画像を加算コンポジットする場合、つまり「N枚の画像の対応するピクセルのカウント値を足し上げる」という操作を考える。ある特定のピクセルに着目し、そのピクセルの\(i\)枚目のカウント値が\(S_i\)、その標準偏差が\(\sigma_i\)だとしよう。加算コンポジット後の合計カウント値を\(S_{total}\)、その標準偏差を\(\sigma_{total}\)と置くと、まず\(S_{total}\)は以下の式で書ける。 \begin{align*} S_{total} = S_1 + S_2 + \cdots + S_N\\ \tag{2}\end{align*} (2)式中の各\(S_i\)はそれぞれノイズを含んでいるので、合計された\(S_{total}\)もノイズを含んでいる。誤差の伝播の公式(1)に当てはめてコンポジット後のノイズを求めてみると、 \begin{align*} \sigma_{total} &= \sqrt{\left( \frac{\partial S_{total}}{\partial S_1} \right)^2 \sigma_1 ^2 + \left( \frac{\partial S_{total}}{\partial S_2} \right)^2 \sigma_2 ^2 + \cdots + \left( \frac{\partial S_{total}}{\partial S_N} \right)^2 \sigma_N ^2}\\ &=\sqrt{\sigma_1 ^2 + \sigma_2 ^2 + \cdots + \sigma_N ^2}\\ &\unicode{x2252} \sqrt{N} \bar{\sigma} \tag{3}\end{align*} となる。ただし各\(\sigma_i\)の平均値\(\bar{\sigma}=\frac{\sigma_1 + \sigma_2 + \cdots + \sigma_N}{N}\)とした。この式からわかるように、\(N\)枚を加算コンポジットするとノイズは \begin{align*} \bar{\sigma} \rightarrow \sigma_{total} = \sqrt{N} \bar{\sigma} \tag{4}\end{align*} となり、増えることがわかる。一方で\(S_{total}\)は\(N\)枚を加算したことにより \begin{align*} S_{total} = N \bar{S_i}\\ \tag{5}\end{align*} と、単純にN倍になった。 \begin{align*} \bar{S_i} \rightarrow S_{total}=N \bar{S_i} \tag{6}\end{align*} ここで\(\bar{S_i}\)は平均値\(\bar{S_i}=\frac{S_1 + S_2 + \cdots + S_N}{N}\)である。この\(S_total\)と\(\sigma_{total}\)からS/Nを計算してみると \begin{align*} S/N = \frac{S_{total}}{\sigma_{total}} &= \frac{N\bar{S_i}}{\sqrt{N}\bar{\sigma_i}}\\ &= \sqrt{N} \frac{\bar{S_i}}{\bar{\sigma_i}} \tag{7}\end{align*} となり、\(N\)枚をコンポジットすると、１枚のS/Nよりも\(\sqrt{N}\)倍だけS/Nが良くなる事が分かります。これがまさにコンポジットの意義であり、コンポジットを行うとどんどんS/Nが良くなっていくのだ。

 

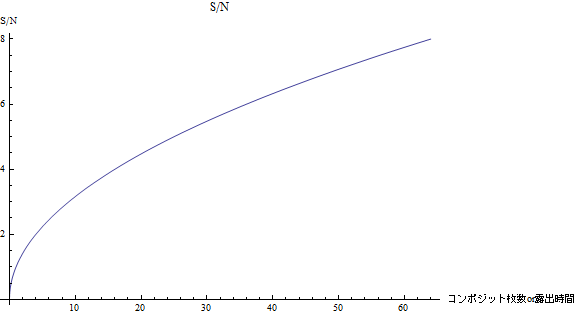
図２：コンポジット枚数とS/Nの関係