
本シリーズでは様々なシーンで利用される干渉計について、その原理や応用例などを解説する。前回に引き続き、トワイマン・グリーン干渉計について紹介する。
本シリーズの記事はこちらから:
さまざまな干渉計:干渉計の分類
さまざまな干渉計:フィゾー干渉計(1)
さまざまな干渉計:フィゾー干渉計(2)
さまざまな干渉計:フィゾー干渉計(3)
さまざまな干渉計:トワイマン・グリーン干渉計(1)
さまざまな干渉計:トワイマン・グリーン干渉計(2)
さまざまな干渉計:トワイマン・グリーン干渉計(3)
今回の記事を読み進める前に、ぜひとも前回の記事の記事を一読いただきたい。
今回は前回に引き続きトワイマン・グリーン干渉計のビームスプリッタに求められる面精度について解説する。図1はトワイマン・グリーン干渉計のビームスプリッタの面精度が悪い時、すなわち各面で厚みの誤差(\(\delta_{t1}, \delta_{t2}, \delta_{t3}\))がある場合の光線図である。
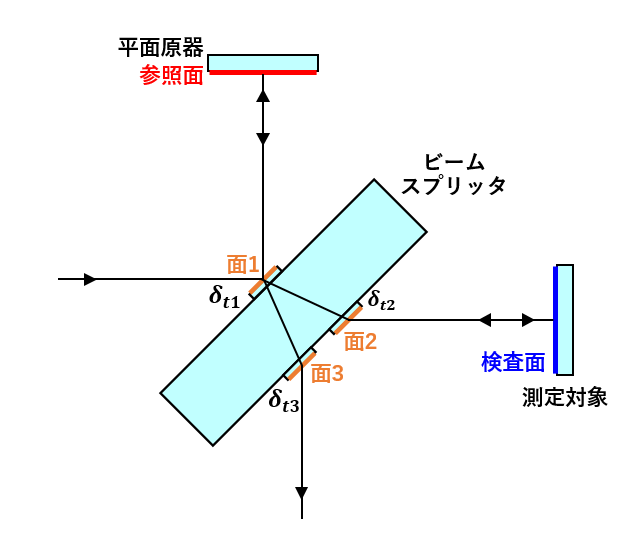
図1:ビームスプリッタに厚みの誤差がある場合の光線図
参照面と検査面を通る2光路は、各面を以下のように反射・通過をして伝搬していく。
・参照面を通る光路A:面1を反射 ➡ 参照面を反射 ➡ 面1を通過 ➡ 面3を通過
・検査面を通る光路B:面1を通過 ➡ 面2を通過 ➡ 検査面を反射 ➡面2を通過 ➡ 面1を反射 ➡ 面3を通過
ここで前回導出した、斜入射した光が面を反射・通過する際に発生する光路差OPD(Optical Path Difference)に関する式(1)および(2)を図2に示す。これらの式を使って「参照面を通る光路A」と「検査面を通る光路B」で発生する光路差からビームスプリッタに求められる面精度を算出する。
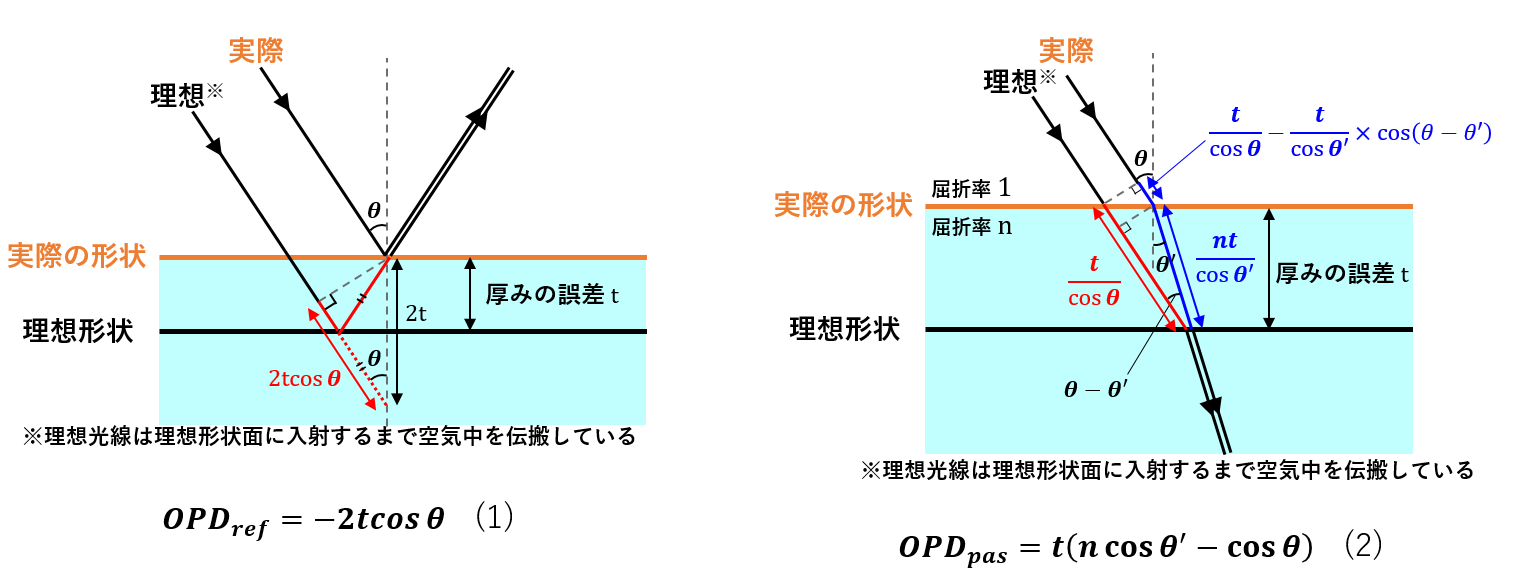
図2:斜入射した光の反射後の光路差(左)と通過後の光路差(右)
各光路で面1~3に関連する反射・通過について式(1)、(2)を代入すると、
\begin{align}
OPD_A &= -2\delta_{t1}\cos{\theta} + \delta_{t1}(n\cos{\theta^{\prime}}-\cos{\theta}) + \delta_{t3}(n\cos{\theta^{\prime}}-\cos{\theta}) \tag{3} \\
OPD_B &= \delta_{t1}(n\cos{\theta^{\prime}}-\cos{\theta}) + \delta_{t2}(n\cos{\theta^{\prime}}-\cos{\theta})\times 2 + 2n\delta_{t1}\cos{\theta^{\prime}} + \delta_{t3}(n\cos{\theta^{\prime}}-\cos{\theta}) \tag{4}
\end{align}
光路Aと光路Bの差がビームスプリッタによって生じる光路差\(\text{OPD}_{\text{BS}}\)であるので、式(3)と(4)の差分をとる。そうすると各式の一部の項が相殺され、(5)式で表せる。
\begin{align}
OPD_{BS} &= OPD_{A} – OPD_{B} \\
&=-2\delta_{t1}(n\cos{\theta^{\prime}}+\cos{\theta}) – 2\delta_{t2}(n\cos{\theta^{\prime}}-\cos{\theta}) \tag{5}
\end{align}
ここで、ビームスプリッタの傾きを\(\theta=45^{\circ}\)として屈折率\(n=1.5\)の材質を用いる場合を考える。屈折角は\(\theta^{\prime}=28.1^{\circ}\)となり、これらを式(5)に代入すると以下のようになる。
$$ OPD_{BS} = -4.1\delta_{t1} – 1.2\delta_{t2} $$
これより光路差\(\text{OPD}_{\text{BS}}\)は、面1の形状誤差\(\delta_{t1}\)の影響を強く受け、その影響は面2の\(\delta_{t2}\)に比べておよそ3.4倍大きい。よって、面1は面2に比べて高精度に研磨しておく必要がある。例として、測定精度\(\lambda/10\)で検査面を測定する時を考える。このとき\(\text{OPD}_{\text{BS}}\)は\(\lambda/20\)程度にする必要があるが、これを達成するには仮に面2の誤差\(\delta_{t2}\)が0であったとしても、面1の誤差は\(\delta_{t1} \sim \lambda/82\)とする必要があり、非常に高精度な研磨が要求されることとなる。現代であればビームスプリッタの面精度が低くても、計算機上で系統誤差として減算することで高精度な測定が可能である。しかし計算機の存在しない時代では、トワイマン・グリーン干渉計の測定精度はビームスプリッタの形状誤差(特に面1)によって測定精度が低下していた。
次回はマッハ・ツェンダー干渉計について紹介する。

趣味は天文と写真と車。大学では天文サークルに所属し、暗い空を求めて日本中を飛び回っていた。 天文学を極めるために大学院に進学、在籍中は中間赤外線分光器の開発に従事。 カメラやレンズに関する記事を主に担当。