コリメーションチェッカーを使用できる光線の波長幅

コリメーションチェッカーの原理などは過去の記事で紹介しているので、ぜひ本記事を読み進めるにあたり復習をお願いしたい。
調整された平行光ってどれくらい平行なの？　コリメーションチェッカーの調整限界（１）
調整された平行光ってどれくらい平行なの？　コリメーションチェッカーの調整限界（２）
調整された平行光ってどれくらい平行なの？　コリメーションチェッカーの調整限界（３）

コリメーションチェッカーを使用することが可能な光線の波長幅を求めるには、干渉を起こす２光線の光学的距離の差が入射光線のコヒーレント長よりも短くなる条件を求めればよい。図１に干渉する光線の詳細図を示す。図１に記載されている２本の赤い光線は概ねコリメートされている、すなわち平面波として入射しているとする。

 

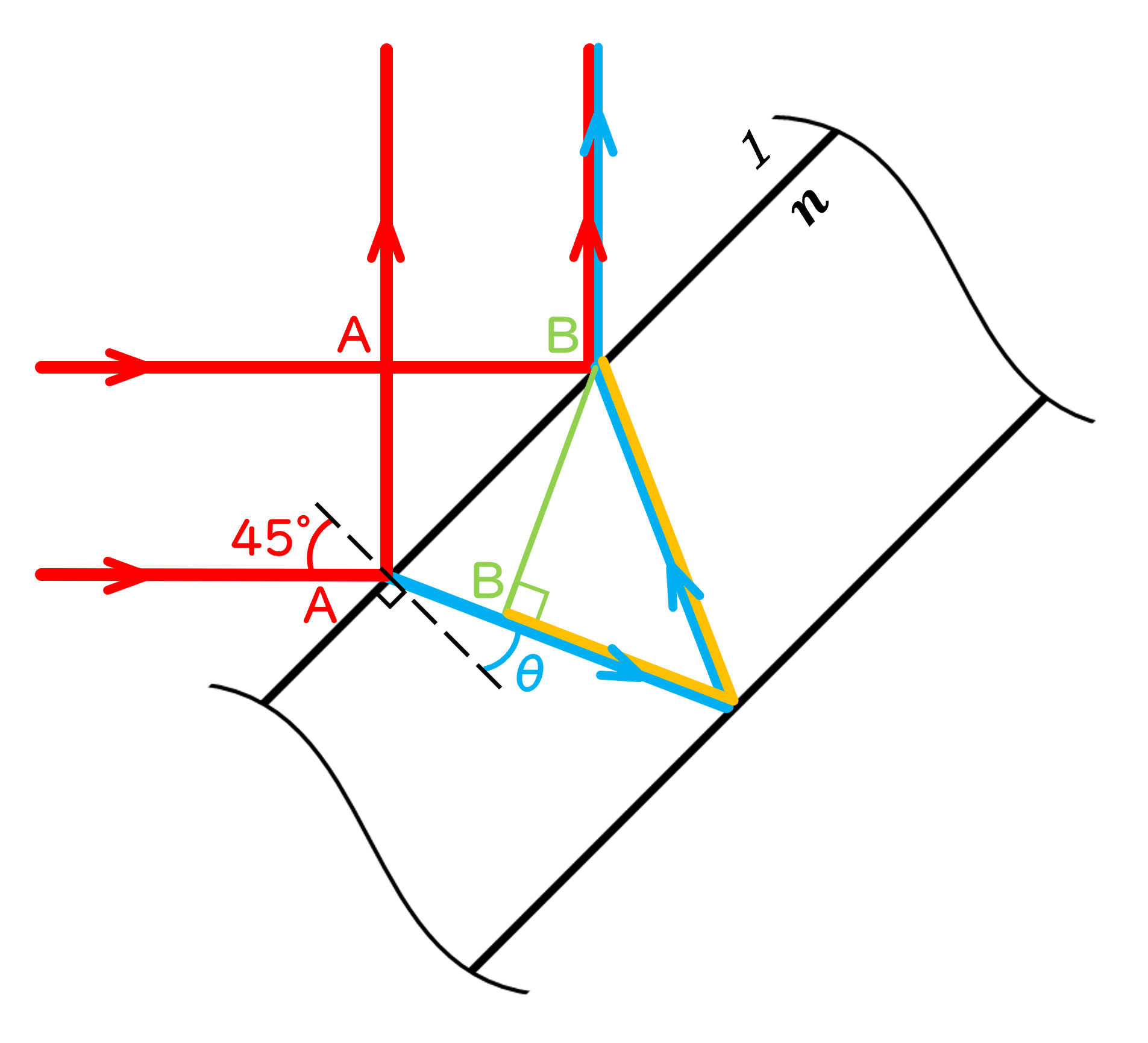
図１：ガラス板に入射して干渉する光線の詳細図。入射光線はコリメート光とする。

 

ガラス板の表面で反射した赤い光線（上側）と裏面で反射した青い光線が出口で出会いスクリーン上に干渉縞を作るとして、赤い光線（上側）と青い光線のの光学的距離の差を考えよう。ある時刻にA–Aの場所に存在した波面は進行し、B–Bの位置に達する。ここで、波面がB–Bの位置に来ることは光線と波面が直交することから分かる。したがって、２光線の光学的距離の差はオレンジの部分で生じていることが分かる。オレンジの部分の幾何学的長さは図２から\(2t\cos{\theta}\)になっていることが分かる。したがって、ガラス板の屈折率を乗じることで光学的距離の差は\(2nt\cos{\theta}\)になる。これが入射光線のコヒーレント長よりも短ければ、２つの光線が干渉しコリメーションチェッカーが機能する。

 

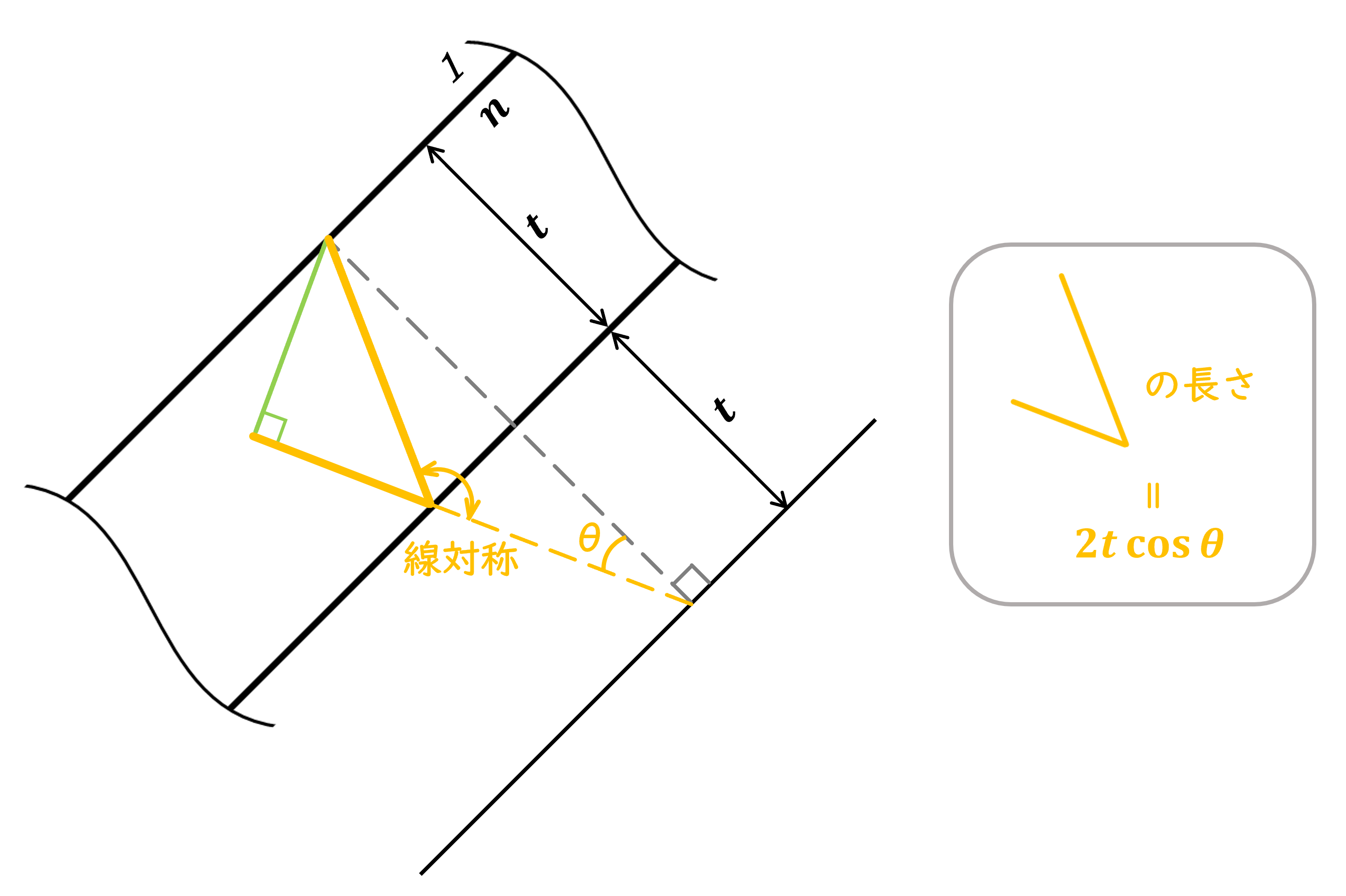
図２：ガラス板に入射して表面反射した光線と裏面反射した光線の光学的距離

 

具体的な例で計算してみよう。たとえば、シグマ光機で販売されている「SPV-25」という型番のコリメーションチェッカーで考えてみる。入射光の波長\(\lambda = 0.5876 [\mu m]\)とする。ガラス板の硝材はBK-7なので、入射光の波長での屈折率は\(n=1.5168\)であり、板厚は5mmである。まず、表面の屈折に対して、スネルの法則から

$$ 1 \times \sin{45^{\circ}} = n \times \sin{\theta} $$

したがって、

\begin{align}
\cos{\theta} = \sqrt{1-\sin ^2{\theta}} & \left( 0 < \theta < \frac{\pi}{2} \right) \\ = \sqrt{1-\frac{1}{2n^2}} \end{align} これより、干渉する２光線の間の光学的距離の差は以下のようになる。 \begin{align} 2nt\cos \theta = 2t \sqrt{n^2-\frac{1}{2}} \\ = 2 \times (5\times10^{-3}) \times \sqrt{1.5168^2 - \frac{1}{2}} \\ \simeq 13.4\times10^{-3} \text{[m]} \end{align} この光学的距離の差がコヒーレント長さよりも短ければよいため、次の条件式が成り立つ。 $$ 13.4 \times 10^{-3} < \frac{\lambda^2}{\Delta \lambda} = \frac{(0.5876 \times 10^{-6})^2}{\Delta \lambda} $$ これを解くと、コリメーションチェッカーを使用可能な波長幅\(\Delta \lambda\)は以下のようになる。 $$ \Delta \lambda < 25.8 \times 10^{-12} \text{[m]} = 25.8 \text{[pm]} $$ ただし、（コヒーレント長）\(=\frac{\lambda^2}{\Delta \lambda} という条件を用いた（コヒーレント長については別記事にて解説する予定だ）。したがって、このコリメーションチェッカーを用いる場合は入射光線の波長幅が25.8[pm]以下である必要があることがわかる。一般のコリメーションチェッカーであっても、概ね同程度の波長幅が要求されると思っておけばよいだろう。 この結果から、太陽光や星の光、電球、蛍光灯、LEDライトなどの連続スペクトルをもつ光源は、そのままではコリメーションチェッカーが使用できないことがわかる。参考までに、典型的なレーザー光源の波長幅を表１に示す。表１からもわかるように、半導体レーザーでは、コリメーションチェッカーの要求する波長幅にはあまり余裕がない。特に波長幅の広い半導体レーザーでは干渉縞が見えないこともあり得るので、注意が必要だ。

 

表１：レーザーの波長幅の例