
本シリーズでは、レンズを使った結像光学系(望遠鏡、カメラ、プロジェクターレンズ等)の光学設計に必要な収差を理解することを目標にする。今回は、歪曲収差について述べる。
本シリーズのこれまでの記事:
ピンボケ、球面収差 光学収差を理解する:単色収差の分類(1)
コマ収差 光学収差を理解する:単色収差の分類(2)
像面湾曲、非点収差 光学収差を理解する:単色収差の分類(3)
歪曲は、像のボケというよりは画像の歪み(=各視野の光線の結像点が焦点面内で不均一にずれること)として現れる収差である。これまで考えてきた収差はある視野点の光線束に注目した際に、その光線束が焦点面で1点に集まらずに、広がりを持つ現象であった。これに対して、歪曲は像の歪みを対象とするため、各視野点から発する光線束内の1本の光線(ふつうは主光線)を追跡することでその現象を理解することができる。多くの結像光学系は、物平面上の各点における光軸からの高さ\(y(=a \tan\theta)\)と像平面上における共役点の光軸からの高さ\(y^{\prime}(=b \tan\theta ^{\prime})\)とが比例関係にあることを理想とする(図1)。この時、像はある倍率で完璧に拡大・縮小される。
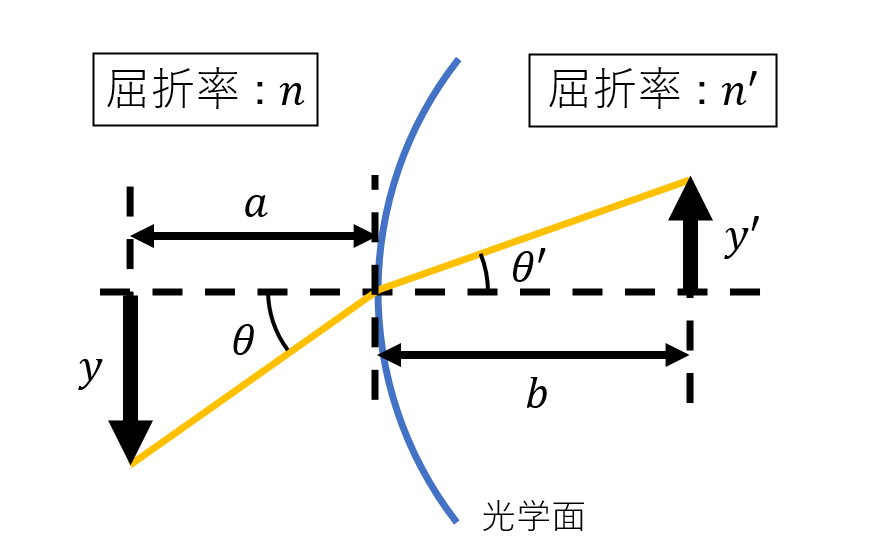
図1:1つの光学面において軸外の主光線の追跡をしたもの。
しかし、屈折の式
$$ n\sin\theta = n^{\prime}\sin \theta ^{\prime} $$
からわかるように、\(\tan\theta\)と\(\tan\theta ^{\prime}\)は比例関係ではないため、\(y^{\prime}\)は\(y\)に対して線形応答ではない。したがって、光学面が多数存在して非線形応答を繰り返す一般的な光学系においても、必ずしも\(y^{\prime}_N\)は\(y_1\)に比例せず(図2の上)、主に\(y_1\)の3乗に比例した大きさでずれる。これが歪曲の正体であり、そのずれの向きによって糸巻型・樽型に分類される(図2の下)。ここで、「必ずしも」といったのは光学面の組み合わせによっては歪曲を消すことができる。その代表例が薄肉レンズだけで光学系が構成され、かつ絞りがレンズ面に一致するように設置されている場合である。この場合、各視野の主光線が薄肉レンズの中心を通過する。薄肉レンズの中心は、局所的に厚さ0の平行平板とみなすことができる。したがって、\(\theta_1\)と\(\theta^{\prime}_N (N=2)\)は等しくなり、ひいては\(y_1\)と\(y^{\prime}_N(N=2)\)が比例関係になるため歪曲は発生しない(図3)。
ここまで、歪曲の発生原理を説明したが、光学設計時には歪曲を許す場合もある。撮像素子としてデジタル画像が取得可能なものを用いた場合は、得られた画像を処理することによって像の歪みを修正できる。
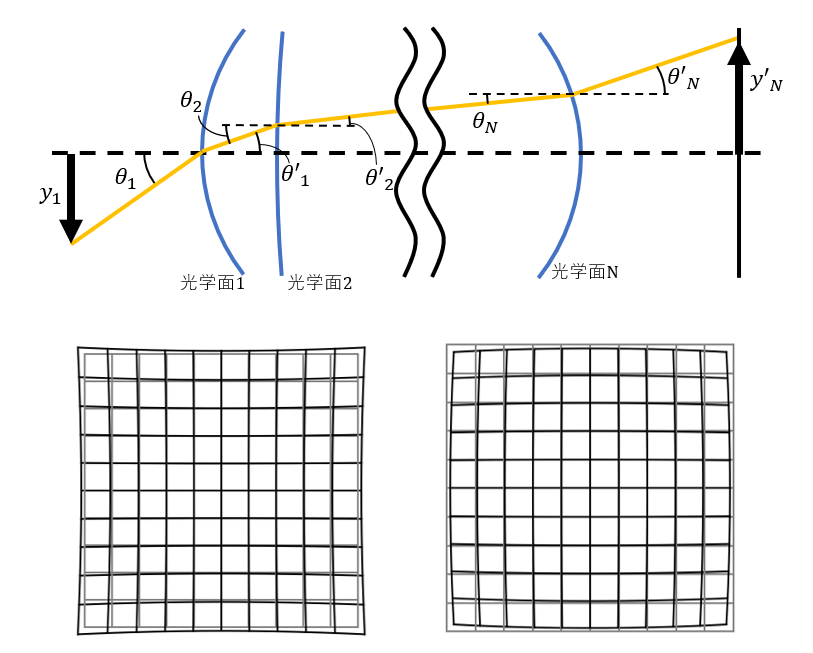
図2:(上)一般的な光学系と軸外の主光線を追跡したもの。(下)左が正方グリッド(灰色)を糸巻き型の歪曲を持つ光学系で投影したもの(黒)、右が正方グリッド(灰色)を樽型の歪曲を持つ光学系で投影したもの(黒)。
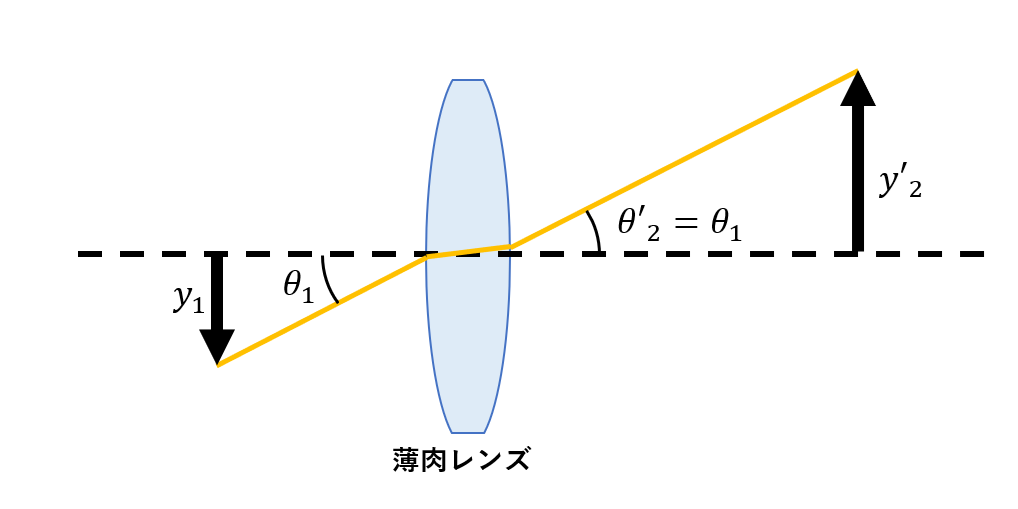
図3:歪曲を持たない薄肉レンズにおいて軸外の主光線を追跡したもの。

京都大学大学院理学研究科 宇宙物理学教室 博士課程在籍。 研究内容は自由曲面を用いた軸外し光学系の開発。