ARコーティングの多層膜化の効用　その２

結局のところ、現実の材料を用いた単層膜では理想的なAR特性が実現できないため、複数の材料を使った薄膜を考えてみよう。図１（左）に示すように、フッ化マグネシウムの単層膜とガラスの間に、酸化アルミニウム（Al₂O₃、n=1.68）のλ/4膜を挿入した２層の膜を考える。

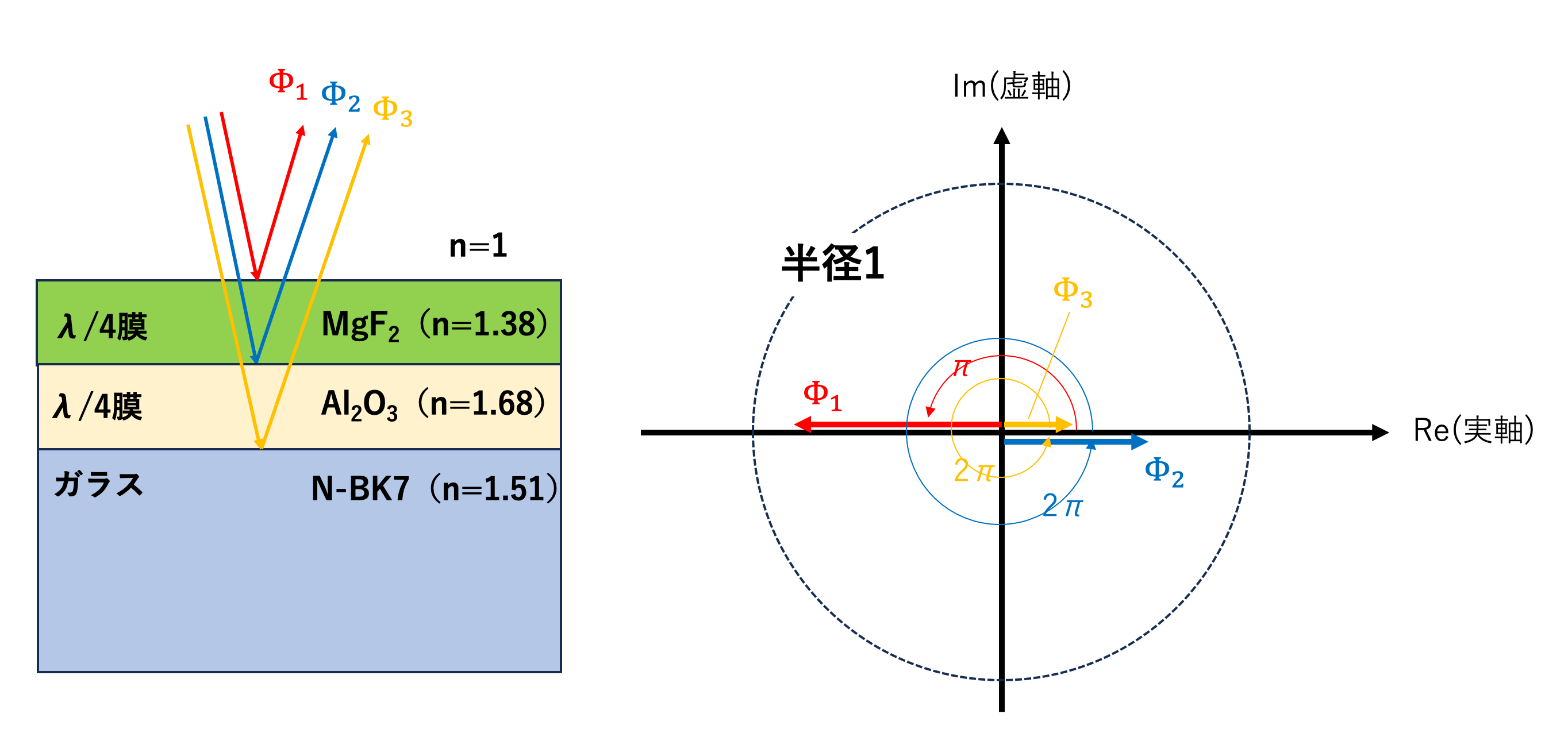
図１：フッ化マグネシウム・酸化アルミニウムの２層の膜の模式図（左）およびそのベクトル図（右）

この場合３箇所の膜界面での反射があるため、それぞれの反射複素振幅を\(\Phi_{1}\)、\(\Phi_{2}\)、\(\Phi_{3}\)とすると、

　　
$$\Phi_{1}= r_{1} \exp(-i0) = \frac{1-1.38}{1+1.38} \exp(-i0) = 0.160 \exp(-i \pi)$$
$$\Phi_{2}= r_{2} \exp(-i \pi) = \frac{1.38-1.68}{1.38+1.68} \exp(-i \pi) = 0.098 \exp(-i 2\pi)$$
$$\Phi_{3}= r_{3} \exp(-i 2\pi) = \frac{1.68-1.51}{1.68+1.51} \exp(-i 2\pi) = 0.053 \exp(-i 2\pi)$$

となる。ここでrは振幅反射率であり、界面前後の屈折率を用いて\(r=\frac{n_{前}-n_{後}}{n_{前}＋n_{後}}\)で計算できる（前回の記事を参照）。これらをベクトル図にプロットしたのが図１（右）である。\(\Phi_{1}\)に対して\(\Phi_{2}\)と\(\Phi_{3}\)が逆向きなので、全てのベクトルを足し合わせたものは、\(-0.160+0.098+0.053=-0.008\)となり、反射率（\(=|-0.083|^{2}\)）はほぼゼロになる。

ベクトル図表（図１）から、一層目表面での反射光である\(\Phi_{1}\)を、二層目の前後の反射光である\(\Phi_{2}\)と\(\Phi_{3}\)の２つの波面で協力して打ち消していることが定性的に理解できる。同膜の分光反射率特性を図２（緑線）に示す。設計波長を500nmとした場合のものであるが、設計波長において単層膜（紫線）に比較して反射率がゼロに近づいていることが分かる。分光反射率特性の曲線の形状から、このタイプのコートはVコートと呼ばれる。

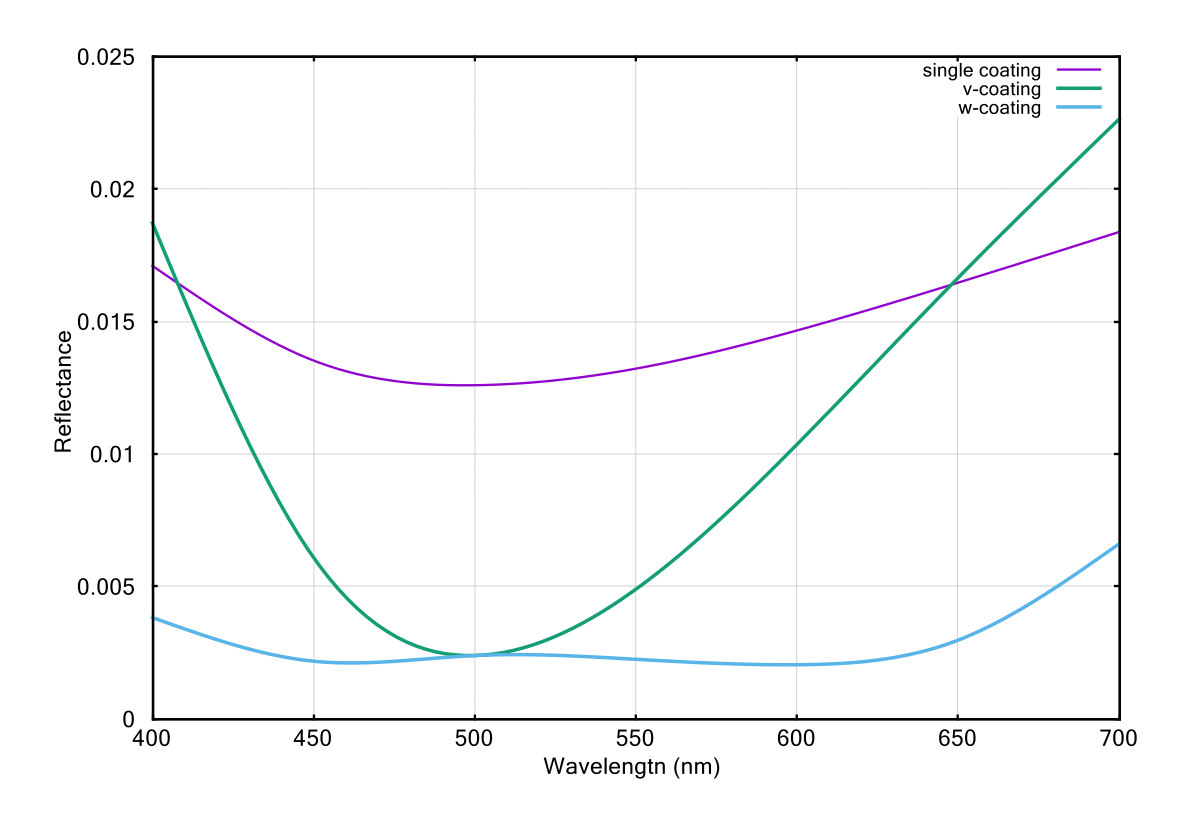
図２：フッ化マグネシウム・酸化アルミニウムによる多層膜コーティング（Vコート）の反射率特性

Vコートでは単層コートに比べて、設計波長の前後の420nm～650nmの範囲で高いAR性能を示していることが図２から分かるが、カメラレンズのように、可視光全域（380nm～700nm）で使用したいときには単層コートよりも特性が悪くなる。これは単層膜に比べて膜厚が厚くなるため、設計波長からずれると急激に位相条件を満たさなくなることが原因である。次回はさらに層を増やしたコーティングについて考察してみよう。