
前回のアッベ数の本質(1)では、レンズの色収差補正に用いられる重要なパラメータである「アッベ数」について、不思議な形の定義を紹介した。今回はこの定義式がなぜこのように表されるのか、解説しよう。
近軸理論によれば、薄肉レンズの焦点距離fは、以下の式(別記事にて回折)によって表すことができる。
$$\frac{1}{f(\lambda)} = \left(n(\lambda)-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$$
ここで\(R_{1}\)と\(R_{2}\)は、レンズの表面と裏面の曲率半径である。ここでは屈折率、すなわち焦点距離には波長依存性があることを強く明示するために、わざわざ\(f(\lambda)\)、\(n(\lambda)\)という表現を用いていることに注意されたい。今、3つの波長\(\lambda_{a}\)、\(\lambda_{b}\)、\(\lambda_{c}\)(ただし\(\lambda_{a} < \lambda_{b} < \lambda_{c}\))を考えると、 $$\frac{1}{f(\lambda_{a})} = \left(n(\lambda_{a})-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$$ $$\frac{1}{f(\lambda_{b})} = \left(n(\lambda_{b})-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$$ $$\frac{1}{f(\lambda_{c})} = \left(n(\lambda_{c})-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$$ が当然成り立つ。ここで、波長\(\lambda_{a}\)と\(\lambda_{c}\)での焦点距離の差\(\Delta f_{ca}\)を考える。上記の3つの式を用いると、 $$\Delta f_{ca} = f(\lambda_{c}) - f(\lambda_{a}) = \left(\frac{1}{n(\lambda_{c})-1}-\frac{1}{n(\lambda_{a})-1}\right)\left(n(\lambda_{b})-1\right)f(\lambda_{b})$$ となる。さらに、 $$n(\lambda_{a}) = n(\lambda_{b}) + \Delta n_{a}$$ $$n(\lambda_{c}) = n(\lambda_{b}) - \Delta n_{c}$$ と置き直し、式を変形すると、 $$\frac{\Delta f_{ca}}{f(\lambda_{b})} = \frac{n(\lambda_{a}) - n(\lambda_{c})}{\left(n(\lambda_{b})-1\right)^{2} + \left(n(\lambda_{b})-1\right)\left(\Delta n_{a} - \Delta n_{c}\right) - \Delta n_{a}\Delta n_{c}}\left(n(\lambda_{b})-1\right)$$ となるが、\(\Delta n_{a} \sim \Delta n_{c} \ll n(\lambda_{b})\)とできるので、分母の第二、代三項は無視することができ、結局のところ $$\frac{\Delta f_{ca}}{f(\lambda_{b})} = \frac{n(\lambda_{a}) - n(\lambda_{c})}{n(\lambda_{b})-1}$$ が得られる。【注:ここでは厳密なテイラー展開を行っていないことが気になる読者の方もおられるかもしれないが、計算結果は等しくなることは付け加えておく。厳密なテイラー展開は光学に関わる物理数学:近似(3)にて。】
この式は(分母と分子は逆であるものの)アッベ数そのものである。左辺の\(\Delta f_{ca}\)は波長\(\lambda_{a}\)と\(\lambda_{c}\)の焦点距離の差(=軸上色収差)を、平均的な焦点距離\(f(\lambda_{b})\)で割ったものになっているので、アッベ数とは「その硝材における単位焦点距離あたりの軸上色収差(の逆数)」であることがわかる。アッベ数は屈折率のみによって決まる量で、硝材が決まれば一意に決まる。したがって、単レンズの単焦点距離あたりの軸上色収差量(=比色収差量)は、硝材を指定すれば、近軸かつ薄肉レンズにおいては、そのレンズ形状によらず決まってしまう、ということを意味している。
図1はオハラ社が提供している研磨レンズ用光学ガラスのマップである。縦軸はd線(587.56nm)での屈折率で、横軸がd線でのアッベ数である。アッベ数は非常に広く分布しており、おおよそ15~95の値をとる。このことから、レンズの比色収差量は硝材の違いによって6.7%(=1/15)~1.1%(=1/95)まで変化することが分かる。
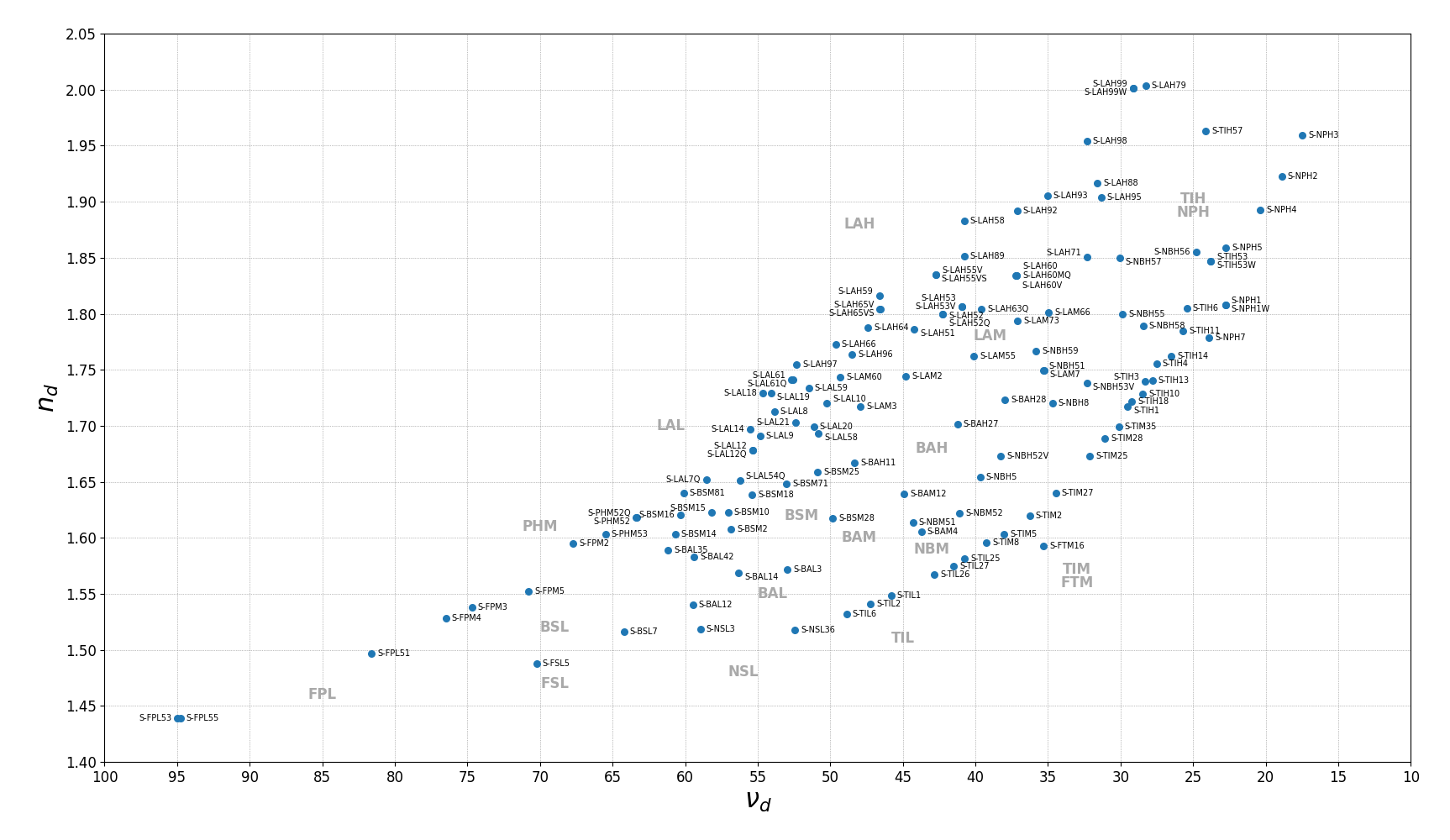
図1:オハラ社で提供されている光学ガラスのマップデータ(2024年3月現在)

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。