
この世の中で、凸レンズと凹レンズどちらが多いだろうか?前回の記事では、光学入門書に解説されている「コバ厚と中心厚の比較による判定法」では、説明がつかない事例があることを紹介した。ではどのような関係を満たすときか?レンズの焦点距離の公式を使って考えてみる。
曲率半径が\(R_{1}\)と\(R_{2}\)、屈折率\(n\)、中心厚\(d\)のレンズの焦点距離\(f\)は以下の式で表される(前回の記事(2)式)。
$$ \frac{1}{f} = \left(n-1\right) \left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) + \frac{\left(n-1\right)^2}{n}\frac{d}{R_{1}R_{2}} \tag{2}$$
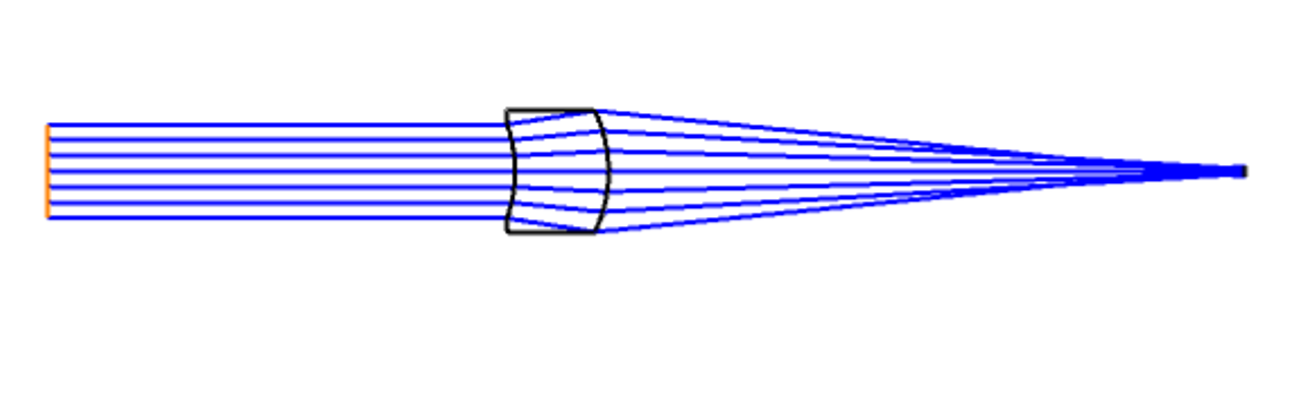
図1:\(R_{1}=-30\)mm、\(R_{2}=-30\)mmのメニスカスレンズの光路図
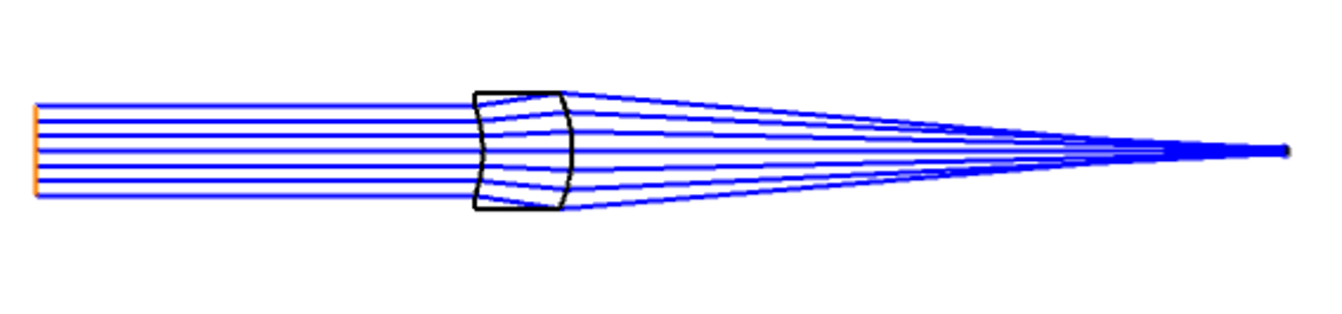
図2:\(R_{1}=-30\)mm、\(R_{2}=-31\)mmのメニスカスレンズの光路図
今興味がある凸/凹レンズの判別法が通用しないのは、図1と図2を参考にするとおそらく\(R_{1} \sim R_{2}\)の場合であろうと考えられる。そこで、微小量\(\Delta R\)を用いて\(R_{2}=R_{1}+\Delta R\)とする。このとき、焦点距離の式は以下のように変形できる。
\begin{align}
& \frac{1}{f} = \left(n-1\right) \left(\frac{1}{R_{1}}-\frac{1}{R_{1}+\Delta R}\right) + \frac{\left(n-1\right)^2}{n}\frac{d}{R_{1}\left(R_{1}+\Delta R\right)} \\
&\sim \frac{n-1}{\left(R_{1}\right)^2} \left\{ \Delta R \left(1-\frac{1}{R_{1}}\frac{n-1}{n}d\right) + \frac{n-1}{n}d \right\} \tag{3}
\end{align}
ただし、式変形では\(\frac{\Delta R}{R_{1}} \ll 1\)を仮定した。\(f > 0\)となるために\(\Delta R\)が満たすべき条件を求めると、
$$ \Delta R > -\frac{A}{1-\frac{A}{R_{1}}} \tag{4}$$
$$ \left(\text{ただし} A = \frac{n-1}{n}d\right) $$
が得られる。つまり、このとき凸レンズとなる。ここで、(\(n > 1\)なので)\(A > 0\)であり、またレンズ内に焦点が形成されるような特別な場合を除くと\(\left(1-\frac{A}{R_{1}}\right) > 0\) であることがわかるので、式(4)の右辺は負の値になることが分かる。つまり、凸レンズであっても\(\Delta R\)が負の値を取りうる(\(R_{2} > R_{1}\)になりうる)ことがある、ということである。もう少し整理すると、\(-\frac{A}{1-\frac{A}{R_{1}}} < \Delta R < 0\)の範囲にあるとき、凸レンズ(\(f > 0\))であっても、
ことが生じる、ということになる。なお、多くの場合はレンズの中心厚\(d < |R_{1}|\)なので\(A \ll R_{1}\)であり、このとき\(\Delta R > -A\)と非常に簡単な形になる。さらに\(n=1.5\)とすると\(\Delta R > -A = -\frac{2}{3} d\)であるので、目安として第一面と第二面の差が中心厚の2/3を下回る時は、見た目は凹レンズなのに凸レンズの場合が存在するということになる。
なぜこのようなことが起こるのかを図1と図2を見ながら定性的に考えてみたい。図では入射面(\(R_{1}\)面)が凹面であるため、レンズ内の光線は拡散光となって進む。レンズの中心厚が厚くなると、入射面(\(R_{1}\))に比べて射出面(\(R_{2}\))で光線高は非常に大きくなるため、より角度の大きい面での屈折を受けることになる。その結果として(曲率半径がほぼ同じであっても)光線は集光し、凸レンズとして振る舞うことになる。入射面が凸面の場合は、射出面(凹面)での光線と屈折がより小さくなるため、凸面で発生する屈折角がより勝った結果として光線は集光し、やはり凸レンズになる。
ここでようやく最初の命題に戻る。式の乱出によって、なんのための議論かもはや忘れさらえてしまったかもしれないが、ここまでで分かったのは「外形から判定すると凹レンズに見えるが、実は凸レンズという場合が存在する」、ということである。逆に「見た目は凹レンズだけど実は凸レンズ」というものが存在しないことは、凹レンズになる条件式は式(4)の符号を逆にしたであることから推測できる。(絶対にこんなことはあり得ないことは承知しているが)もしこの宇宙にすべての曲率半径のレンズが均等な分布で存在するとすれば、外形では凹レンズと判断されるレンズのの一部は実は凸レンズであることになるので、「原理的には(全宇宙を見渡すと)凸レンズの方が多いはず」という結論になる。なお、なぜこうした非対称性が生まれるのか。これは、レンズ厚が正の値しかとれない(負の厚みのレンズが存在しない)からである。その証明は読者に任せたい。

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。