反射光における位相のジャンプ：固定端と自由端（２）

ここで、光が進む媒質同士の界面においては、以下の条件が成り立つとして考えを進めてみよう。

1. ①波面位相が連続である
2. ②エネルギーが保存する

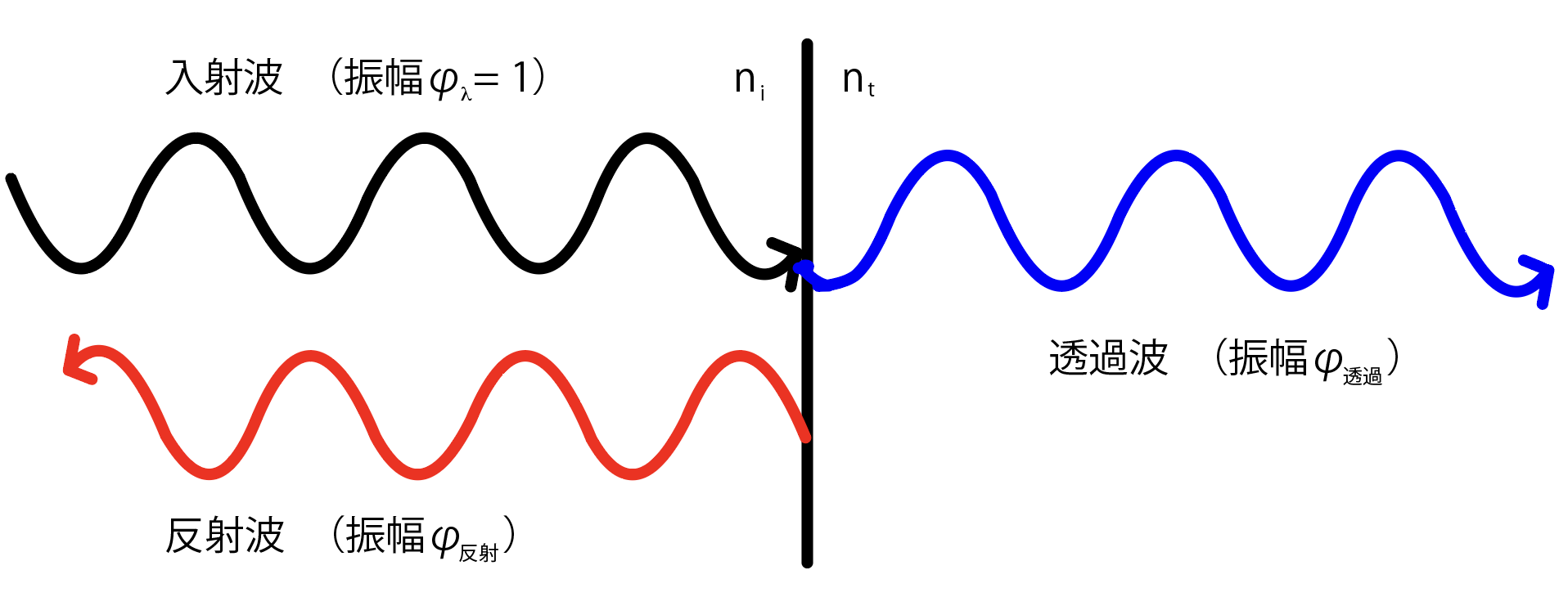
ある時刻における入射波面の振幅（\(\phi_{\lambda}\)）を1、透過波面の振幅を\(\phi_{透過}\)、反射波面の振幅を\(\phi_{反射}\)（図１）とすると、上記の２つの条件から以下の関係を満たす必要がある。
$$ 1 + \phi_{反射} = \phi_{透過}　・・・(1) $$
$$ n_{i} ×1 = n_{i}{\phi_{反射}}^{2} + n_{t}{\phi_{透過}}^{2}　・・・(2) $$　
なお（１）式は条件①より、（２）式は条件②より定式化される。（２）式において、複素振幅の大きさの２乗に屈折率がかかっているのは、電磁波のポインティングベクトルの考察から得られる結果である（別稿をにて解説予定）。ここで、横軸に\(\phi_{反射}\)、縦軸に\(\phi_{透過}\)をとった直交平面を考えると、（１）式は傾き１、切片が１の直線（-1 < \(\phi_{反射}\) < 1）、（２）式は、\(\phi_{反射}\)軸の半長が1、\(\phi_{透過}\)軸の半長が\(\sqrt{n_{i}/n_{t}}\)の楕円の式になっていることが分かる（図２）。反射波面と透過波面は２つを同時に満たさなければならないことから、２つの線の交点が得られるべき反射波と透過波の振幅ということになる。交点の位置は、楕円の形状が変化するため\(n_{i}/n_{t}\)によって変化していく。

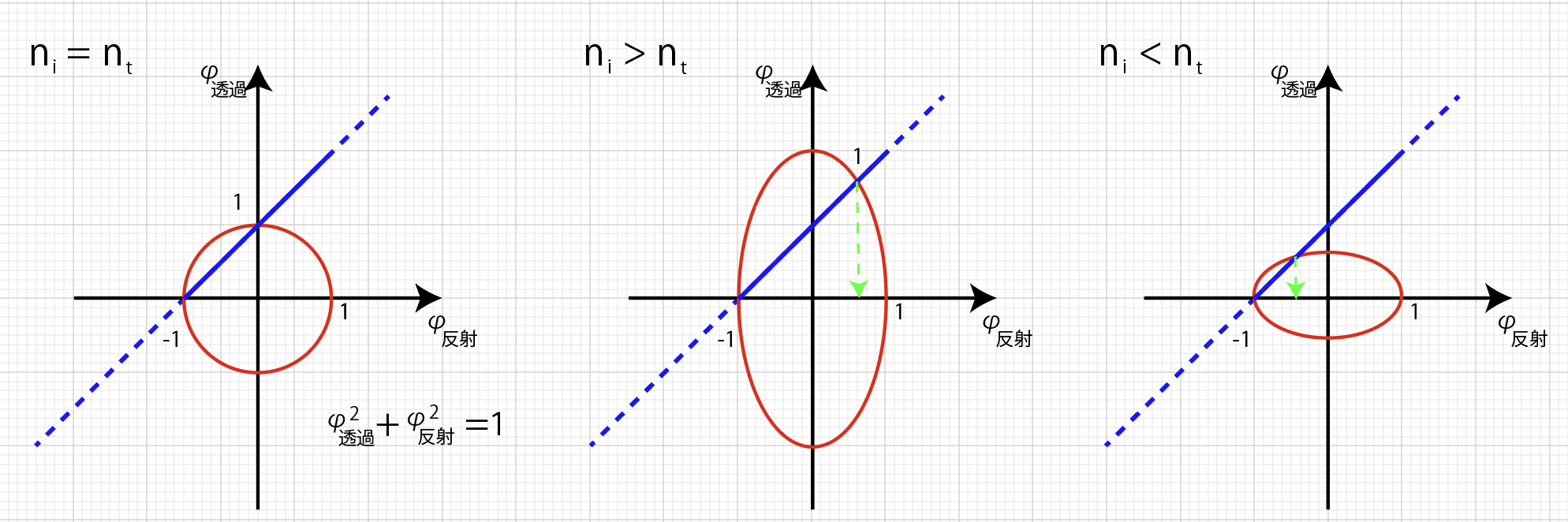
まず、特別な場合として\(n_{i}/n_{t}=1\)（つまり\(n_{i}=n_{t}\)）の場合を考える。このとき、楕円は半径１の円になるので、直線との接点は\(（\phi_{反射},\phi_{透過}）=（0, 1）\)となる。\(n_{i}=n_{t}\)では界面自体が存在しないことと同じなので、反射波の振幅がゼロになり、透過波の振幅が1になるはずで、確かにそうなっていることが分かる。次に\(n_{i}/n_{t} > 1\)（\(n_{i} > n_{t}\)）の場合は、楕円は\(\phi_{透過}\)軸に延びた形状になる。その結果、反射波においては\(\phi_{反射} > 0\)の場所に接点が移ることが分かる。逆に、\(n_{i}/n_{t} < 1\)（\(n_{i} < n_{t}\)）の場合は、楕円は\(\phi_{透過}\)軸に潰れた形状になるため、反射波においては\(\phi_{反射} < 0\) の場所に接点が移る。\(\phi_{反射}\)符号が負であるのは、位相が半波長ずれていることを表すので、たしかに\(n_{i} > n_{t}\)の場合は位相ずれは発生しないが、\(n_{i} < n_{t}\)になると位相が半波長ジャンプすることがこの図から見て取れる。

結局のところ、屈折率界面において位相がジャンプすることがあるのは、界面において「位相の連続」と「エネルギー保存」の２つの辻褄合わせをした結果であると言える。\(n_{i} < n_{t}\)の場合においては、透過波の強度が小さくなっていくが、エネルギー保存を維持するためには、反射波の強度を高くする必要がある。その場合、反射波の振幅も大きくなるが、入射波と反射波が同位相では位相の連続性から透過波の振幅が大きくなりすぎてしまう。そこで、反射波の位相を反転させて入射波の振幅を打ち消すようにして矛盾を解消した、というのが真相である。改めて、波の賢さに感嘆する次第である。