
光路長が丁度λ/4の厚さになる薄膜である「λ/4膜」。ガラス面に積層することで、ARコートとして反射率を抑える役割だけでなく、反射率を増加させ「ミラー」を構成することも可能である。前回の記事では、多層膜によってミラーとなる原理を紹介したが、「基準波長λ以外ではミラーとして機能するのか?」という疑問も同時に産まれる。今回はベクトル図を用いてこの疑問について考えてみたい。
波長λ+Δλにおけるm番目の層の下面からの反射光の複素振幅は以下で表現される。
$$\Phi_{m} = A_{m} \exp\left[2 \pi i \frac{m\lambda}{2(\lambda+\Delta\lambda)}\right] \quad\text{for}\quad m=2j-1 \quad(j=1,2…)$$
$$\Phi_{m} = A_{m} \exp\left]2 \pi i \left(\frac{m\lambda}{2(\lambda+\Delta\lambda)} + \frac{1}{2}\right)\right] \quad\text{for} \quad m=2j \quad(j=1,2…)$$
mが奇数の場合は、j番目のペアの\(n_{h}\)膜の下層からの反射光、mが偶数の場合はj番目のペアの\(n_{l}\)膜の下層からの反射光を表す。
式をよく眺めてみると、まず位相(指数関数の肩の数値)は、mが大きくなるにつれて\(\Delta\lambda\)の分だけ\(\pi\)(=180度)からのずれが大きくなっていくことが分かる。これは先に予想した通りだろう。その一方で、振幅\(A_{m}\)には、次第に小さくなっていくだろう。つまりは、\(A_{1} > A_{2} > … > A_{m} > A_{m+1}\)である。その理由は、波面が界面を通過するたびにその一部のエネルギーが反射されて失われていくからである。これらをベクトル図で示すと図1のようになる。多層膜の最上部での反射光のベクトル図を基準にすると、mが大きくなるにつれて(深い膜になるにつれて)ベクトルは回転していくが、同時にその長さは短くなっていく。もし、ベクトルが大きく回転する前に(例えば90度回転する前に)、長さが十分に短くなれば、位相がずれることによって弱め合う効果はほとんど発揮されることなく、高い反射率を維持することができる。Δλが十分に小さい範囲においては、位相ずれは大きくないので、その条件が十分に満たされ、結果的にλからずれた波長においても高い反射率が維持される。一方、Δλがある程度大きくなると、回転角度が大きくなるので(早々に90度を超えてくるので)、波面同士の打消し合いの効果が発揮され、むしろ反射率は小さくなる。

図1:多層膜の場合のベクトル図
反射率を高めるためには、より多くの反射波面で強め合うことが必要になるので、層数が増えるほど反射率は高くなる。この効果は、基準波長からΔλずれた波長でより顕著になる。総数が少ない範囲においては、振幅\(A_{m}\)が大きいため位相ずれによる打消し効果が相対的に大きくなるからである。その結果、層数が少ない膜の反射率の分光特性は基準波長を中心としたなだらかな曲線を描くが、層数が増えるにつれ反射帯は高い反射率を維持したまま平坦にる。Δλが大きいと、強め合う条件が維持されなくなるので急激に反射率が低下し、結果的に矩形に近い分光特性になっていく(図2)。こうした多層膜は特定の波長帯のみを反射することになるので、この性質はバンドパスフィルターにも応用できる。
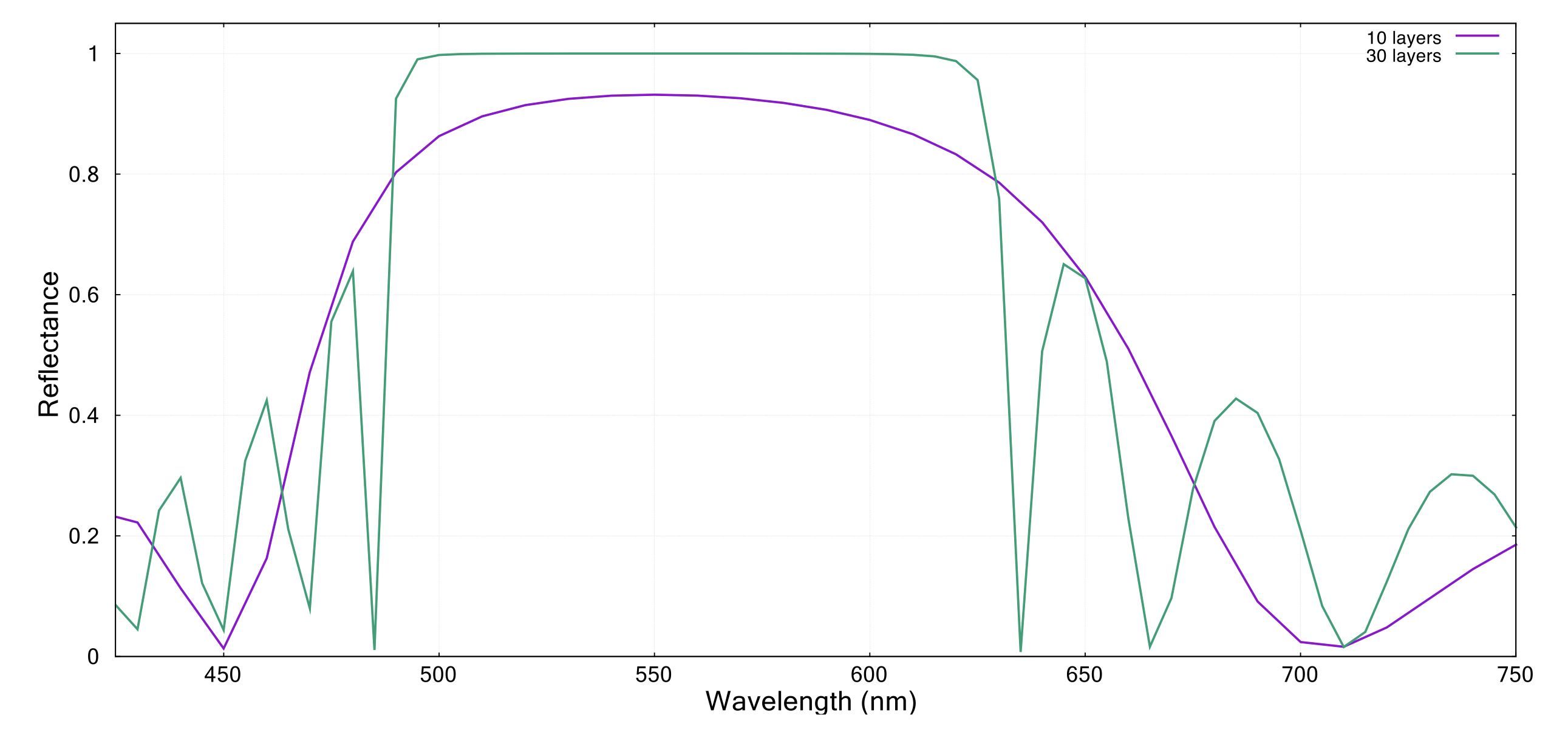
図2:膜数が10層の場合(紫)と30層の場合(緑)の反射率特性
「膜数が増えるほど高い反射率が実現できる」とはいうものの、膜数が増えるとベクトルの回転によって若干の打消しの効果も表れてくるわけなので、その意味では膜数は少ないことに越したことはない。少ない層数で高い反射率を実現するためには、\(n_{h}\)膜と\(n_{l}\)膜の屈折率差(\(\Delta n = n_{h} – n_{l}\))を大きくするとよい。Δnを大きくするほど層界面当たりの反射率(\(=\left(\frac{n_{h} – n_{l}}{n_{h} + n_{l}}\right)^2\))が大きくなるため、同じ反射率を得るにも少ない層数で達成することができる(図3)。また、同じ反射率であれば反射帯域を広げることにもつながる。つまり、より性能のよい反射多層膜を実現するには、\(n_{h}\)膜にはより屈折率の高い材料を、\(n_{l}\)膜にはより屈折率の低い材料を用いれば良いことになる。\(n_{h}\)膜としてはかなり屈折率の大きいTiO2(n=2.4)やTa2O5(n=2.2)が、\(n_{l}\)膜としては屈折率が最も小さい膜種であるSiO2(n=1.4)が良く使われるのはそうした理由による。
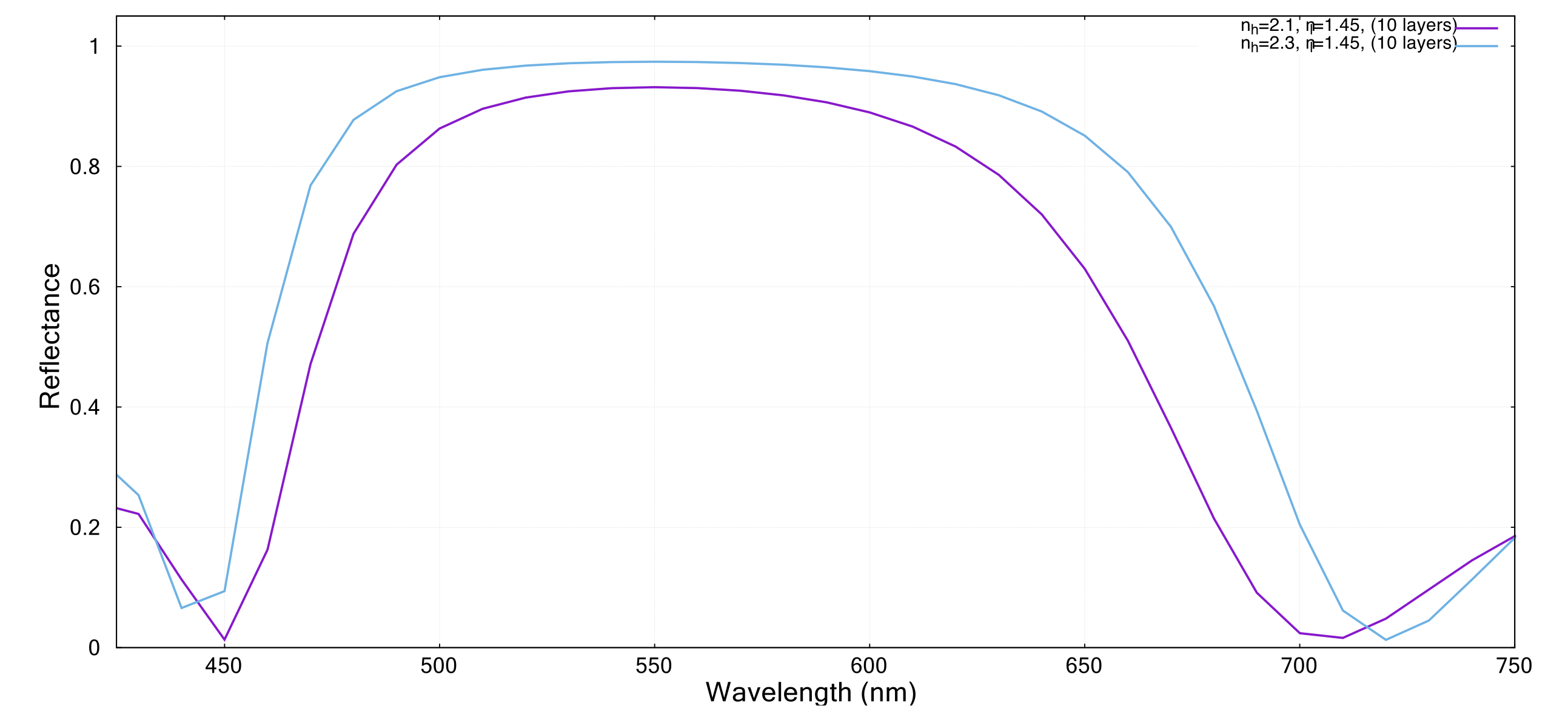
図3:膜屈折率が\(n_{h}\)=2.1と\(n_{l}\)=1.45(Δn=0.65の場合:紫)と\(n_{h}\)=2.3と\(n_{l}\)=1.45(Δn=0.85の場合:水色)の反射率特性
なお、反射多層膜においては注意すべきことがある。図2から分かるように、反射率はある波長帯域に対して100%に近い高い反射率を得ることができるが、その位相(ベクトル図において全てのベクトルを足し合わせた時の角度)は基本波長のそれからは大きくずれている。これは波長に対する位相の変化が小さい金属膜とは大きく異なる性質である。位相の波長依存性が大きいということは、位相の入射角度依存性も大きくなることは容易に想像できる。この事実は、多層膜反射ミラーを収束光(拡散光)中に挿入したり、曲面ミラーに適用する際に問題になる。そのような場合、ミラー面に一様な膜厚で多層膜が施されていたとしても、ミラーの場所によって光線の入射角度が異なるため、異なる位相差が発生し、それらが波面収差となって表れるのである。膜形成前にどんなに高精度の研磨を行なったとしても、多層膜がその努力を台無しにしてしまうのだ。

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。