波面収差の定量化：波面収差の定義とその定式化（２）

おさらいではあるが、光学系が回転対称かつ（光軸を含んだ）平面対称である場合、波面収差関数は以下の形式で記述できる。

\begin{align}
W(\vec{\rho}, \vec{H}) =\
& W_{000} + W_{020}(\vec{\rho} \cdot \vec{\rho}) + W_{111}(\vec{H} \cdot \vec{\rho}) + W_{200}(\vec{H} \cdot \vec{H}) \notag \\
& + W_{040}(\vec{\rho} \cdot \vec{\rho})^2 + W_{131}(\vec{H} \cdot \vec{\rho})(\vec{\rho} \cdot \vec{\rho}) + W_{220}(\vec{H} \cdot \vec{H})(\vec{\rho} \cdot \vec{\rho})　\notag \\
& + W_{222}(\vec{H} \cdot \vec{\rho})^2 + W_{311}(\vec{H} \cdot \vec{H})(\vec{H} \cdot \vec{\rho}) \notag \\
& + W_{400}(\vec{H} \cdot \vec{H})^2 + \cdots
\end{align}

この展開式において\(n=i+j\)をその項の”次数”と呼ぶ。

\(n=0\)（０次）の項

\(n=0\)（０次）の項は\(W_{000}\)のみである。\(W_{000}\)は視野\(\vec{H}\)、瞳座標\(\vec{\rho}\)のいづれにも依存しないことからわかるように、注目する波面が理想球面波に対して相似である状況に相当し、像面上でボケを作らない（図１）。つまり、波面収差の定数成分であり、波動光学における初期位相の項に相当する。したがって、干渉計のような波面の絶対位相が重要になるアプリケーションを除き、多くの場合は無視される項である。

 

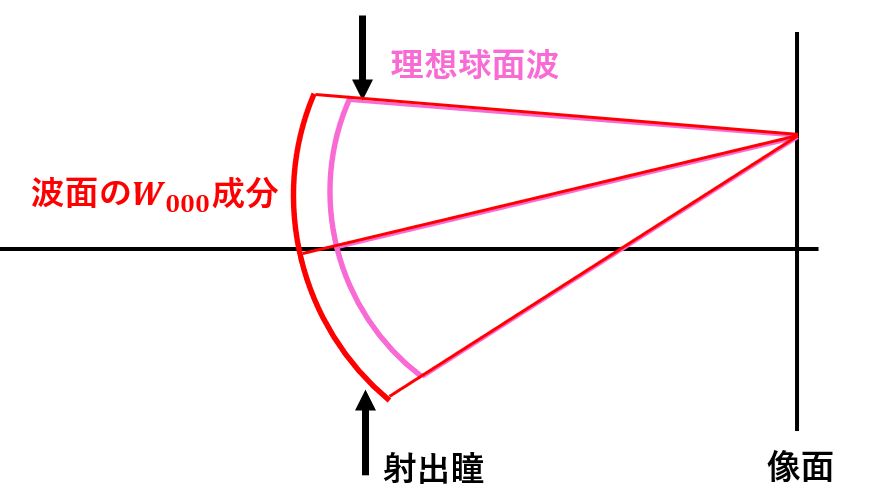
図１：\(W_{000}\)の波面収差の断面図

 

\(n=2\)（２次）の項

\(n=2\)（２次）の項は\(W_{200}(\vec{H} \cdot \vec{H})\)と\(W_{111}(\vec{H} \cdot \vec{\rho})\)と\(W_{020}(\vec{\rho} \cdot \vec{\rho})\)である。まず\(W_{200}(\vec{H} \cdot \vec{H})\)から考える。この項は、\(\vec{\rho}\)の依存性を持たない。したがって、\(W_{000}\)で説明したように波面収差の定数成分になる。\(W_{000}\)との違いは、その定数成分が視野の２乗に比例して大きくなることだが、これは視野ごとの光路長の違いを表している。インコヒーレントな結像の場合は、視野間に光路差があっても像面上でボケを作らないので、多くの場合は無視される項である。次に、\(W_{111}(\vec{H} \cdot \vec{\rho})\)を考える。この項を式変形すると\(W_{111}(\vec{H} \cdot \vec{\rho})=W_{111}(H_x\rho_x+H_y\rho_y)\)となり、\(\vec{H}\)を固定したとき\(\vec{\rho}\)の1次式となることが分かる。したがって、図２の左に示すように波面収差の傾斜成分を表すものである。この成分を持つとき、波面は形状を保ったままその向きを変えることになるため、それによって像面での結像点の位置が変化するだけである。また、そのずれ量は視野中心からの距離に比例して大きくなる（図２の右）。以上より、\(W_{111}(\vec{H} \cdot \vec{\rho})\)は評価する光学系の近軸横倍率が想定したもの（例えば設計値）からずれている状態に相当する。最後に、\(W_{020}(\vec{\rho} \cdot \vec{\rho})\)について考える。この項を式変形すると\(W_{020}(\vec{\rho} \cdot \vec{\rho})=W_{020}(\rho_x^2+\rho_y^2)\)となり、放物面形状をした収差であることが分かる。波面に放物面形状が不可されると、結像位置の光軸方向のずれ、すなわちデフォーカスが発生する（図３）。また、この項に\(\vec{H}\)が含まれないことから、デフォーカス量は視野一様であり（図３の右）、つまりピンボケの効果を波面ベースで見たものに相当することが分かる。

 

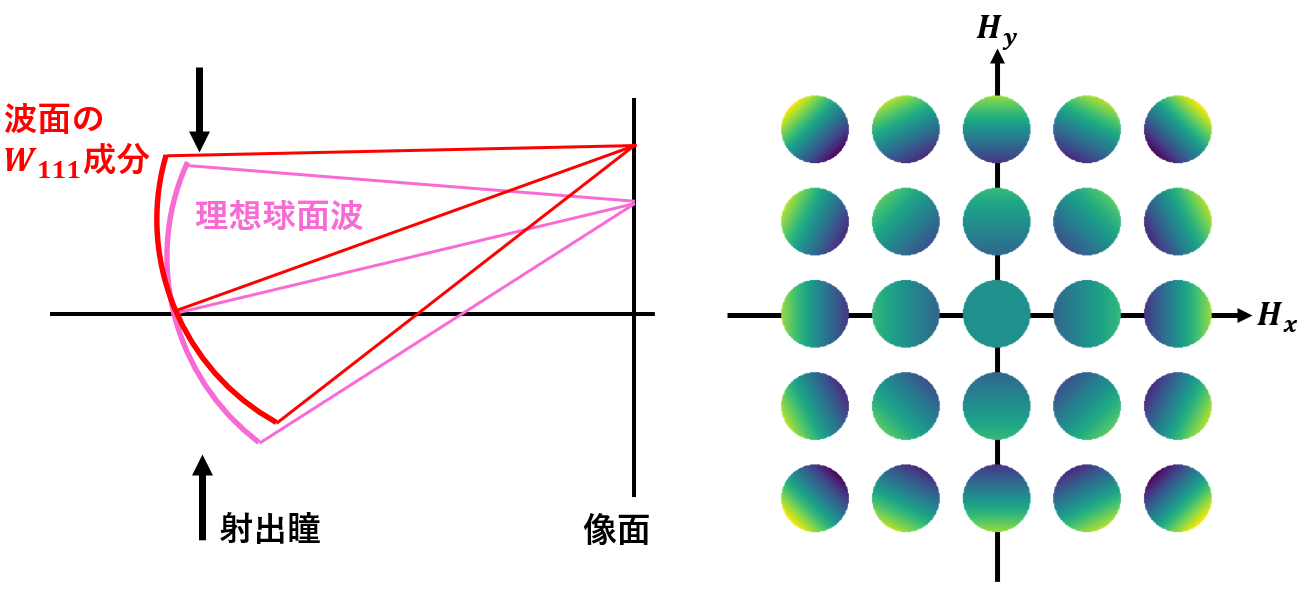
図２：（左）\(W_{100}\)の波面収差の断面図
（右）視野の各点での\(W_{100}\)の形状をカラーマップでプロットしたもの

 

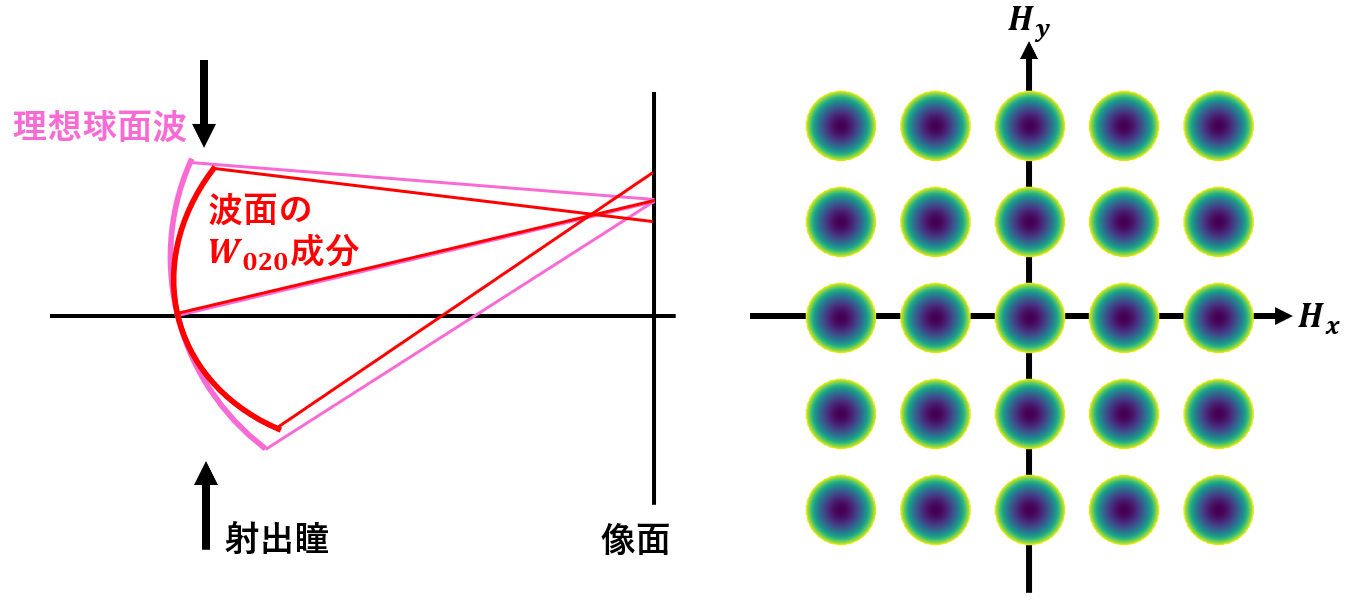
図３：（左）\(W_{020}\)の波面収差の断面図
（右）視野の各点での\(W_{020}\)の形状をカラーマップでプロットしたもの