今回は光学、特に波面の議論においてしばしば登場するZernike多項式の定義に関する話を取り上げたい。Zernike多項式は光学において現れる軸対象な光学収差を解析的に取り扱う際によく用いられる。Zernike多項式の定義は数学的には自然なのだが、そのままの形で用いるのは光学アプリケーションにおいて不便な場合がある。そこでいくつかの表現が提唱され、用いられている。ただしその表現には様々な「流儀」が存在し、現場においては多くの混乱が発生しているようにも見受けられる。そこで本記事ではいろんな場所で使われている「流儀」をできるだけ網羅的に解説してみたい。
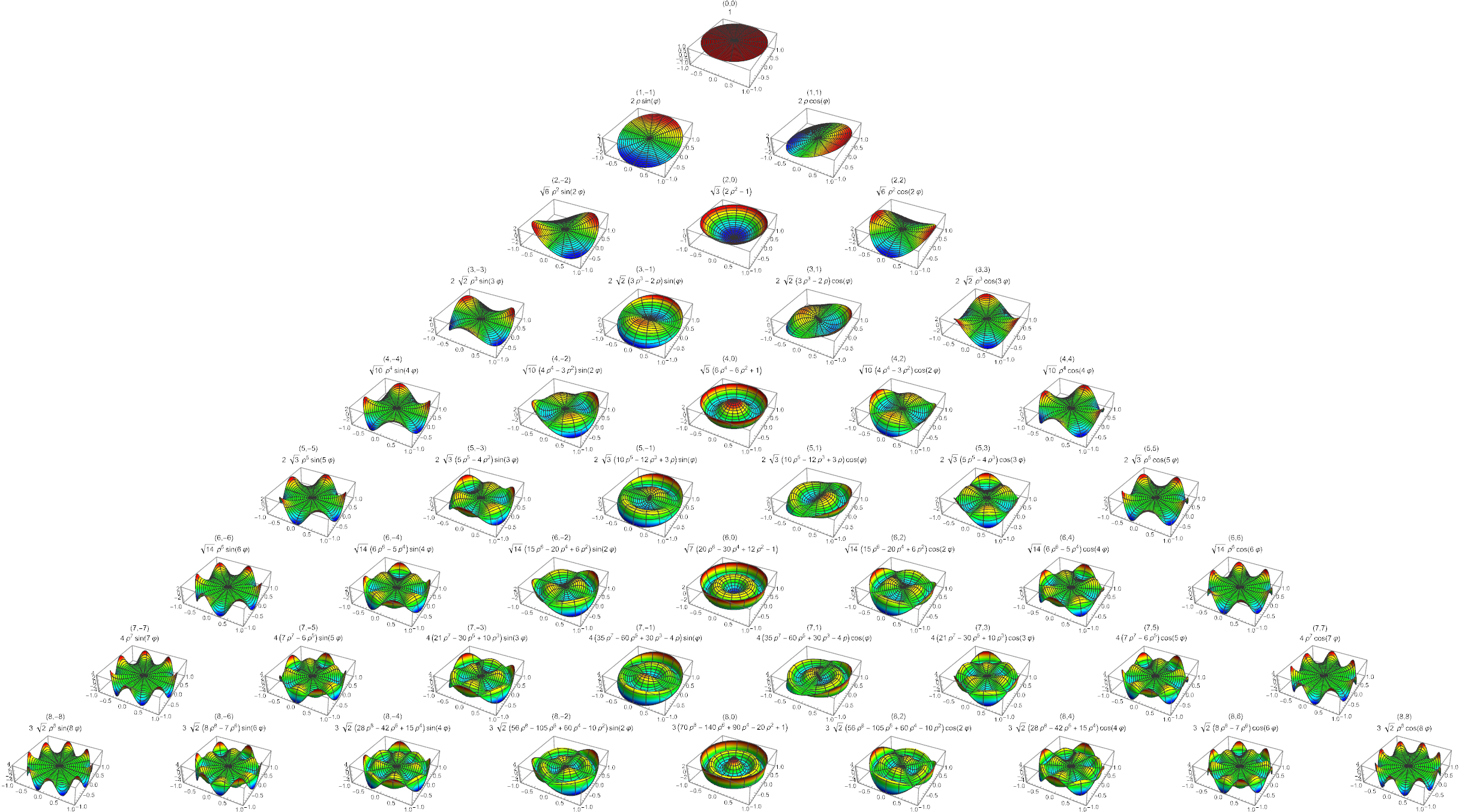
Zernike多項式は一言でいうと「2次元単位円内で定義される正規直交多項式」である。この数学的な意味や取り扱いについては別記事に譲るが、本来のZerike多項式はこのような形をしている。
\begin{align}
Z_n^m(\rho, \varphi) &= N_n^m R_n^{|m|}(\rho)
\begin{cases} \sin(-m \varphi) & (m < 0)\\
\cos(m \varphi) & (m \geq 0) \end{cases}\\
N_n^m &= \sqrt{\frac{2(n+1)}{1+\delta_{m,0}}}\\
R_n^{|m|} (\rho) &=
\begin{cases}
\sum_{k=0}^{\frac{n-|m|}{2}}\frac{(-1)^k (n-k)!}{k!\left(\frac{n+m}{2}-k\right)! \left(\frac{n-m}{2}-k\right)!} \rho^{n-2k} & (n-|m|) \text{が偶数}\\
0 & (n-|m|) \text{が奇数}
\end{cases}
\end{align}
ここで注目したいのが、Zernike多項式の各項は\((n, m)\)という2つの整数(インデックス)で表現されるということである。光学のアプリケーションにおいては波面の解析・制御において線型代数を用いることが多いが、その場合に各項の係数\(C_{n,m}\)が2つの整数\((n, m)\)で決まるのは、一次元ベクトルとして扱いにくいために都合が悪い。そこで1つの整数\(j\)のみで各項の係数\(C_j\)を表現する複数の「流儀」が提唱されている。さらにZernike多項式の各項に掛かる係数\(N_n^m\)についても、上式のとおり表す「流儀」もあれば、こちらを1とする「流儀」もある。こちらの流儀は「スケーリング」といい、前者をRMS正規化、後者をZero-to-Peakスケーリング(0tPスケーリング)という。以下にその中でもよく知られているものを列挙した。
CONTENTS
1976年に大気乱流によって引き起こされる波面乱れの統計的解析を行うために、Robert John Nollが定義したのがNoll方式である。その後、多くの研究者に広く使われるようになり、最も標準的な表現としてその地位を確立するようになった。光線追跡ソフトウェアのZEMAXにおいても”Standard Zernike Polynomial”という名称で採用されている。スケーリングはRMS正規化であり、1次元インデックス\(j\)は(1)式で与えられる。
\begin{align}
j = \frac{n(n+1)}{2} + \lvert m \rvert +
\begin{cases}
0 & \left( mが正かつnを4で割った余りが0か1の場合\right)\\
0 & \left( mが負かつnを4で割った余りが2か3の場合 \right)\\
1 & \left( mが0以上かつnを4で割った余りが2か3の場合 \right)\\
1 & \left( mが0以下かつnを4で割った余りが0か1の場合 \right)
\end{cases}\tag{1}
\end{align}
1999年に人間の目の収差を記述する目的で、OSA(Optical Society of America、現Optica)が定義した方式。後にこの定義は”ANSI Z80.28″(ANSI:American National Standards Institute)、”ISO 24157″として規格として制定された。光線追跡ソフトウェアのCOMSOL Ray Optics Moduleではこの方式がZerike多項式として使われている。スケーリングはRMS正規化であり、1次元インデックス\(j\)は(2)で与えられる。
\begin{align} j = \frac{n(n+2)+m}{2}\tag{2} \end{align}
光線追跡ソフトウェアCodeVで”Standard Zernike”として用いられている定義。スケーリングはZero-to-Peakであり、1次元インデックス\(j\)は(3)式で与えられる。
\begin{align} j = \frac{n(n+2)-m}{2}+1\tag{3} \end{align}
1970年代にアリゾナ大で開発された干渉計で取得された干渉縞の解析を行う”FRINGE”というソフトウェア用にJohn Loomisが定めた定義。USAFと呼ばれることもある。他の1次元インデックスとは大きく異なり、方位角方向の周波数が低いZernike多項式に対して小さな1次元インデックスが割り当てられる。これは、実際の光学系に表れやすい収差を低い次数に割り当てた結果である。また、他の定義と異なり最大で\(j=37\)までしか定義されないという特徴もある。実際、レンズ設計や干渉計測定の解析においては37項あれば十分なことが多い。Zemax、CodeV、OSLOといった光学設計ソフトウェアや、Zygo MetroPro/MXといった干渉計データ解析ソフトウェアなど、多くのソフトウェアで取り扱いが可能になっている。スケーリングはZero-to-Peakであり、1次元インデックス\(j\)は(4)、(5)式で与えられる。
\begin{align}
j =
\begin{cases}
q & (q \leq 36)\\
37 & (q=49;\, n=12, m=0)\\
\end{cases}\tag{4}\\
q = \left( 1 + \frac{n+\lvert l \rvert}{2} \right)^2 -2\lvert l \rvert + \frac{1-\text{sgn}(2m+1)}{2}\tag{5}
\end{align}
Fringe方式を拡張し、\(j=\infty\)項まで項数を増やした定義である。 \(j=1,2, \dots, 36\)まではFringe方式と同じだが、\(j=37\)が異なり、さらに\(j=38\)以降が存在する。スケーリングはZero-to-Peakであり、1次元インデックス\(j\)は(6)式で与えられる。
\begin{align} j = \left( 1 + \frac{n+\lvert l \rvert}{2} \right)^2 -2\lvert l \rvert + \frac{1-\text{sgn}(2m+1)}{2}\tag{6}
\end{align}
Generalized Fringe(GF)方式とほぼ同じであるが、1次元インデックス\(j\)が1つ違いの定義も存在し、それはWyant方式と呼ばれる。スケーリングはZero-to-Peakであり、1次元インデックス\(j\)は(7)式で与えられる。
\begin{align}
j &= j_\text{GF}-1\nonumber\\ &=\left( 1 + \frac{n+\lvert l \rvert}{2} \right)^2 -2\lvert l \rvert + \frac{1-\text{sgn}(2m+1)}{2}-1\tag{7}
\end{align}
ここで紹介した2次元インデックス\((n, m)\)とこれらの1次元インデックス\(j\)の間の対応関係をまとめたものを表1に示す。同じ\(j\)でもZerike多項式の流儀が異なれば、異なる\((n, m)\)に対応するため、Zernike多項式を1次元インデックス\(j\)を用いて表現する場合は、どの方式(流儀)を用いているのかを必ず明記するようにしなければならない。

表1:2次元インデックスと各1次元インデックスの対応

大学院在学中は素粒子物理学を専攻。趣味の天体写真も物理理論に裏付けられた解析方法を行っており、 アマチュア天文家の間で蔓延している都市伝説は一切信じない。赤道儀マニアでアマチュア天文機器にやたら詳しい。 計算機ホログラム(CGH)や干渉計などの高度な物理計算を軽々とこなす。 光学・物理学に関連する原理や数学的理解に関する記事を担当。