分光器の性能を示す主要な仕様項目に"波長分解能"がある。前回の記事では、波長分解能の定義が「どうしてλと∆λの比なのか?」という疑問に対して、光の波長が広いレンジにわたっているためであることを挙げた。今回と次回では定量的な理由について考えたい。
電磁波はその波長によって異なる呼び方がされることは前回述べた通りであるが、スペクトルとして記述した際に、波長にあたる”横軸”も波長域によって様々な表現がなされる。可視光や紫外線、近赤外線領域では横軸は波長(nm)で表現されるが、γ線やX線ではエネルギー(eV)だったり、遠赤外線の領域では波数(cm-1:Kayser)であったり、はたまた電波の領域では振動数(Hz)といった具合である。これらが異なる原因としては、歴史的に使われてきたその波長域の電磁波を検知する検出器の原理に依っているところが大きいと考えられる。「シンプルであることことが美しい」と考えがちな物理学者の立場であれば、これら横軸も今すぐ統一すべきと言うだろうが、そうは問屋が卸さない面もある。変更してしまうと、過去の論文の図表との比較が困難になるといった不都合が生じるのである。いわゆる”技術的負債”と言われるものの類であろう。
横軸が異なる場合、当然ながら波長分解能の解釈も難しくなる。仮に高エネルギーの分野で波長分解能をΔE(eV)と定義されても、可視光領域を主戦場としている研究者や技術者にとっては全くピンとこない。互いに議論を交わしたりする機会がなければそれでもよいかもしれないが、例えば極紫外線(~10nm)のような紫外線とX線の境界領域の場合は、両方の横軸が用いられることがあり、面倒が生じることは避けられない。しかしながら、ここで波長分解能をすべての波長域(横軸)に対してスペクトルの横軸(波長λ、エネルギーE、振動数ν、波数k)で規格化した形で定義すると、
$$R=\frac{\lambda}{\Delta \lambda} = \frac{E}{\Delta E} = \frac{\nu}{\Delta \nu} = \frac{k}{\Delta k}$$
のように、波長分解能の定義はすべて同じ形で書けるのである(このことは光子一個のエネルギーを表す\(E=h\nu=\frac{hc}{\lambda}=hkc\)の式を用いて確認できる)。これは大変好都合である。波長域(分野に)に依らず、波長分解能を議論しやすい数値として定義できることになるからである。
次回の記事では、もう1つ別の理由を紹介する。
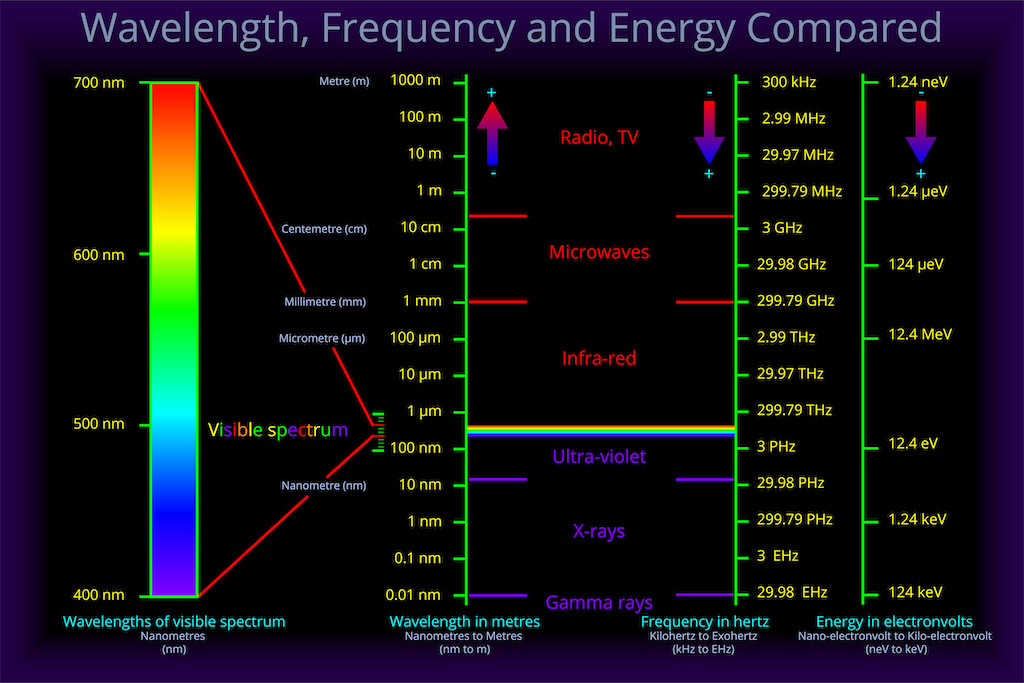
図1:光の波長・周波数・エネルギー

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。