分光器の性能を示す主要な仕様項目に"波長分解能"がある。
分離可能な最小波長幅をΔλminとしたときに、R=λ/Δλminとして定義される。スペクトル中の波長λとλ+Δλの2つの単色光からなる互いに近接したPSF(もしくはLSF)を考える。2つが混じり合った合成PSF(LSF)を観察して、それが2つの波長のPSF(もしくはLSF)から成っていること(=2つの単色光が混じっていること)を何の事前情報もなしに判定できる限界の波長幅が∆λminである。これは顕微鏡レンズなどで使われる空間分解能と基本的に同じ定義である(空間分解能の場合は分離可能な最小距離Δxを以て、分解能と定義ずる)。
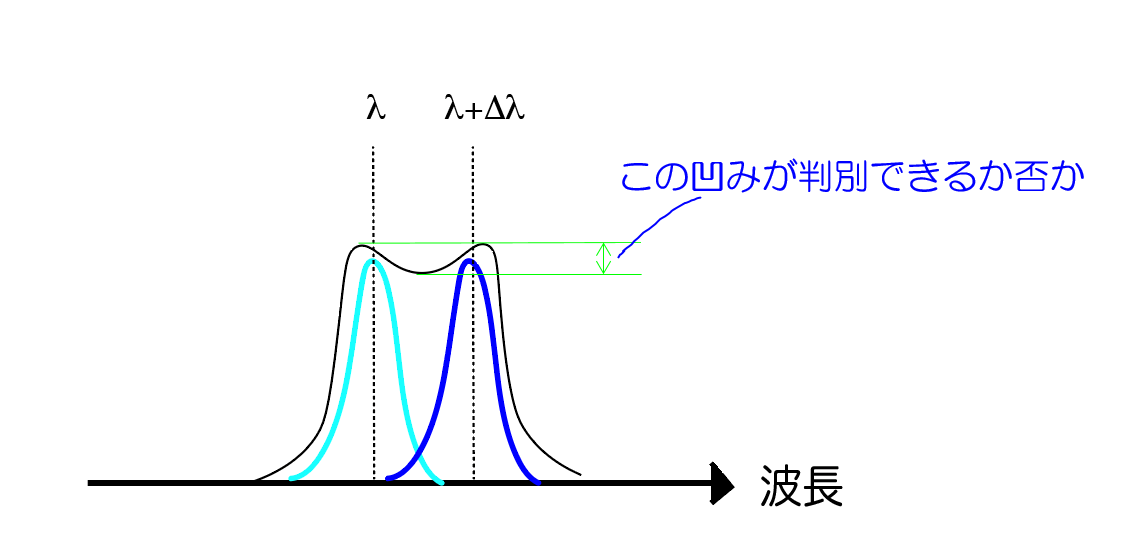
図1:波長分解能の模式図
ところがである。最初にこの波長分解能を学んだ際に、疑問を持った方も多いのではないだろうか?それは「どうしてλと∆λの比なのか?」ということである。「波長分解能が高い=∆λminが小さいこと」からすると、∆λの逆数をとるのはまだ分かるが、空間分解能と同じ考え方なら∆λminだけで定義してしまえば事足りるのではないだろうか。。。?果たして、波長で規格化する意味は?実際に、市販されている様々な分光器のスペック表を見ると(定義に照らし合わせると間違いではあるものの)∆λminを以て”波長分解能”としている例もしばしば見られる。実用上は大きな問題は生じていない、ということでもあろう。今回は、この点について考えてみたい。
まず、考え得る最もシンプルな理由は、「光(電磁波)の波長が数十桁にも渡って存在する」ということである。ご存じのように光は電磁波であり、その波長によって(γ線、可視光、電波のように)異なった呼び方がなされる。そして、波長100mの電波から波長0.00001nm(~100MeV)のγ線まで、波長は14桁も変化する。例えば、可視光域の分光器としてありがちなスペック(波長分解能が”普通”という意味で、”中分散”と呼ばれる)であるΔλminminの数値を聞いただけでは評価が難しい(波長とセットでないと評価できない)という事態になる。その不都合を避けるために、”λと∆λの比”を波長分解能として用いているというわけである。
ただ、おそらくこの説明だけでは納得いかない方も多いだろう。そういう方のために、次回は別の理由を考えてみたい。
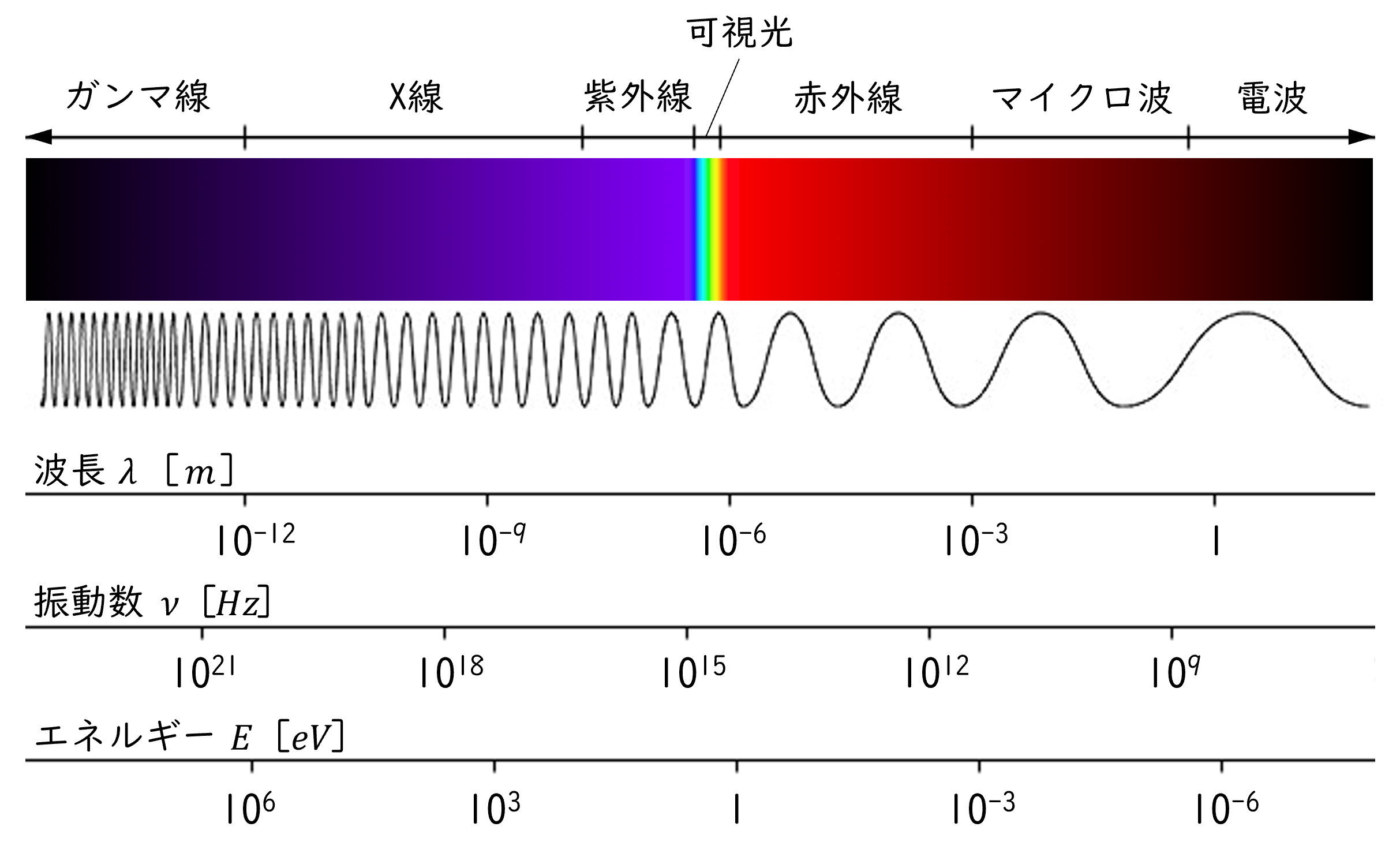
図2:さまざまな波長の光

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。