
前回の記事ではコリメーションチェッカーについて定性的な説明を行った。今回からはいよいよ当初の目的であるコリメーションチェッカーを用いてどこまで完全な平行光線を得ることができるのか?について考えてみたい。
まず、コリメーションチェッカーに入射する(わずかな)球面波を考え、その等位相面を以下によって表現する。
$$\Phi(x,y) = \frac{x^{2} + y^{2}}{2R}\tag{1}$$
ここで、xとyはコリメーションチェッカーの入射面に張った座標系であり、球面波の頂点は原点(x,y)=(0,0)にあるとしている。また、Rは波面の曲率半径である。次に、ウェッジ板の表面と裏面で反射された波面の等位相面を考える。前者については入射波面と同形式になり、
$$\Phi_{表}(X,Y) = \frac{X^{2} + Y^{2}}{2(R+d)} \simeq \frac{X^{2} + Y^{2}}{2R}\tag{2}$$
と表現できる(図1)。式(2)はウェッジ板表面で反射した波面が進行する向きを光軸(Z軸)とし、拡散板上にXY平面を定義した座標系での表現になっていることに注意されたい。xyz座標系とは、\(X/x=1、Y/z=-1、Z/y=1\)という関係が成り立っている(図1)。また、dは入射面から拡散板までの光路長であり、わずかな球面波の場合は\(R \ll d\)であるため、ここでは無視できる。一方で、ウェッジ板の裏面で反射された波面は、ウェッジ板の厚分だけ-Y方向に\(\Delta Y\)だけ位置ずれを起こし、かつウェッジ板の効果によってX軸方向に\(\Delta \theta\)だけ傾いた波面になる(図2)。なお\(d’\)は同じく入射面から拡散板までの光路長であり、\(R \ll d’\)である。
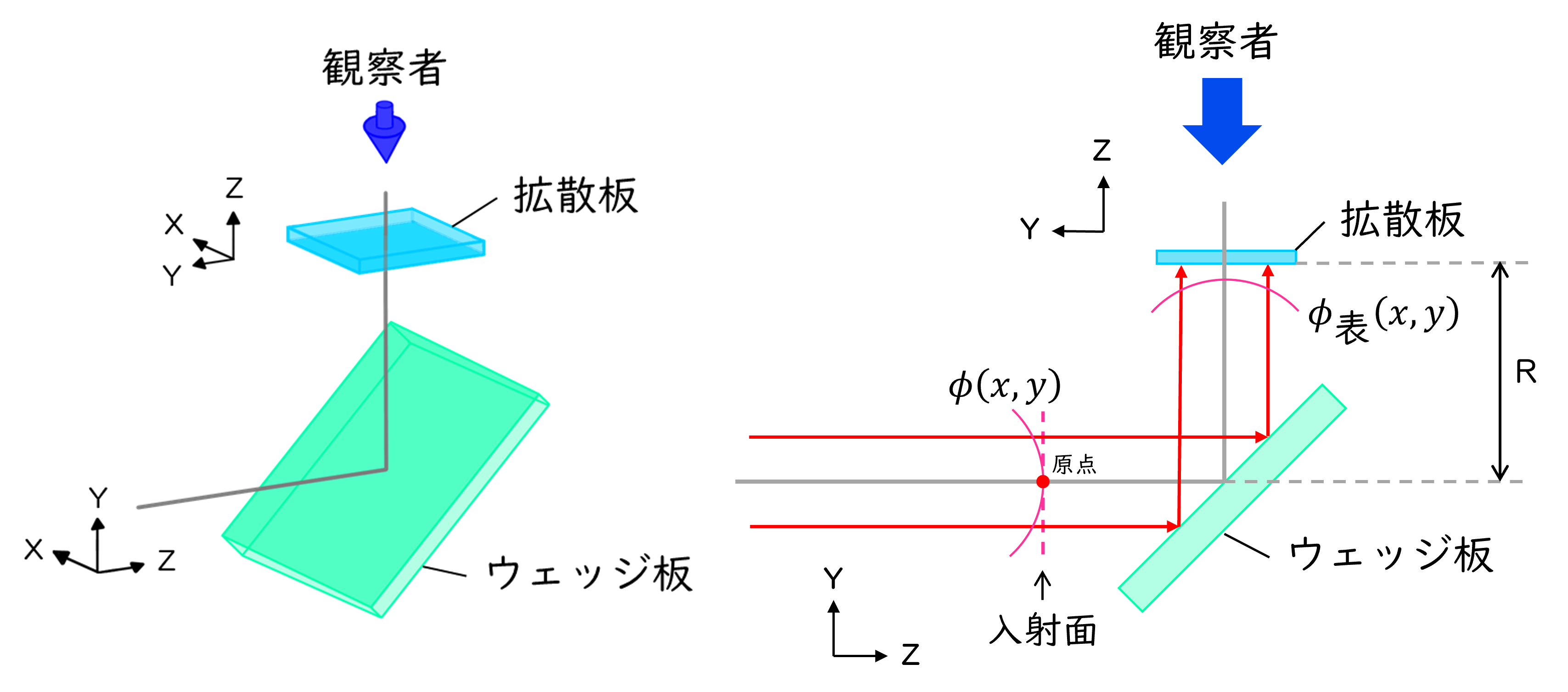
図1:ウェッジ板の表面で反射された波面
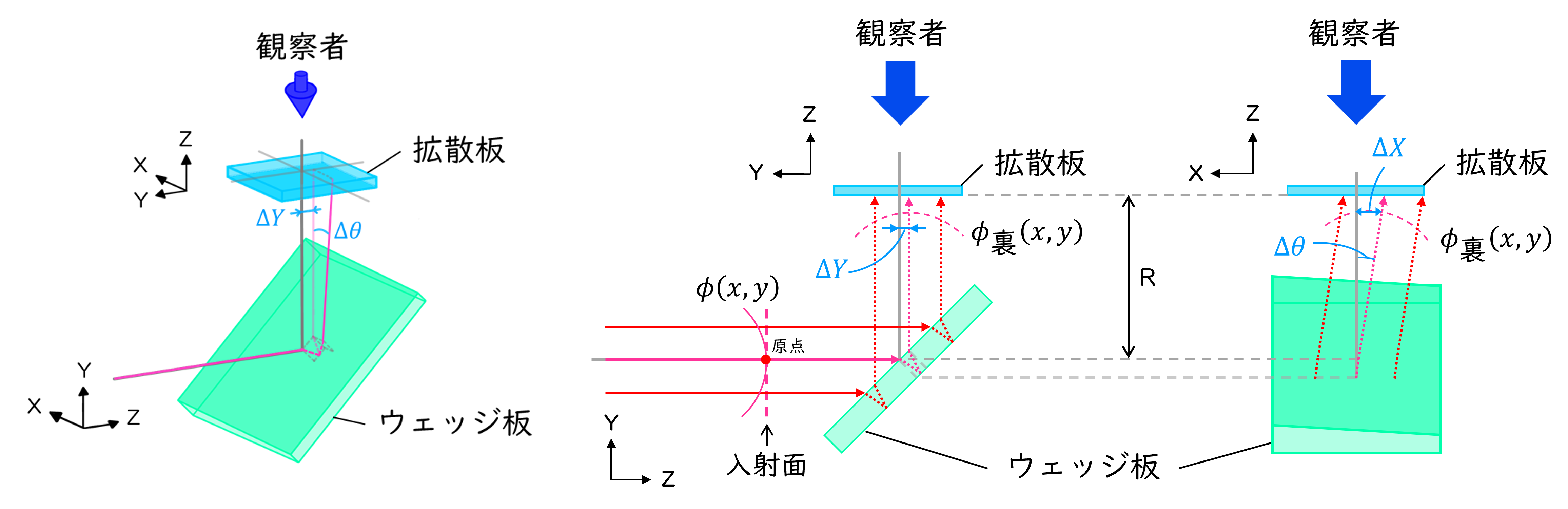
図2:ウェッジ板の裏面で反射された波面
別の記事で得られたとおり、\(\Delta \theta\)だけ傾いた球面波は、\(\Delta X\)だけ平行シフトした球面波とみなすことができ、曲率半径を用いて\(\Delta X \sim R\Delta \theta\)と書ける。この関係を用いると、ウェッジ板の裏面で反射された光は\(\Delta X\)だけ平行シフトしているとみなすことができ、その等位相面\(\Phi_{裏}(X,Y)\)は以下のようになる。
\begin{align}
\Phi_{裏}(X,Y)
&= \frac{(X-\Delta X)^2 + (Y+\Delta Y)^2}{2(R+d’)}\\
&= \frac{(X-R\Delta \theta)^2 + (Y+\Delta Y)^2}{2R}
\tag{3}
\end{align}
拡散板面上においては、2つの波面の位相差\(\Delta \Phi\)(\(=\Phi_{裏}-\Phi_{表}\))が干渉縞にとして局在し視覚化される。今、\(\Delta X/X, \Delta Y/Y \ll 1\)の条件のもとで\(\Delta \Phi\)を計算すると、以下の式が得られる。
$$\Delta \Phi = -\Delta \theta X + \left(\frac{\Delta Y}{R}\right)Y \tag{4}$$
これは、XY座標系における直線の式であり、拡散板には((\Delta \Phi\)が異なる)複数の干渉縞が現れることがわかる。これがコリメーションチェッカーで見られる干渉縞である(図3)。次回は(4)式を用いて、曲率半径と実際に観測される干渉縞との関係、さらにどこまで厳密な並行光が得られるか見ていこう。

図3:コリメーションチェッカーで見られる干渉縞の例

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。