波面収差の定量化：波面収差の定義とその定式化（３）

本シリーズのこれまでの記事はこちらから：
波面収差の定量化：波面収差の定義とその定式化（１）
波面収差の定量化：波面収差の定義とその定式化（２）

おさらいではあるが、光学系が回転対称かつ（光軸を含んだ）平面対称である場合、波面収差関数は以下の形式で記述できる。

\begin{align} W(\vec{\rho}, \vec{H}) =\ & W_{000} + W_{020}(\vec{\rho} \cdot \vec{\rho}) + W_{111}(\vec{H} \cdot \vec{\rho}) + W_{200}(\vec{H} \cdot \vec{H}) \notag \\ & + W_{040}(\vec{\rho} \cdot \vec{\rho})^2 + W_{131}(\vec{H} \cdot \vec{\rho})(\vec{\rho} \cdot \vec{\rho}) + W_{220}(\vec{H} \cdot \vec{H})(\vec{\rho} \cdot \vec{\rho})　\notag \\ & + W_{222}(\vec{H} \cdot \vec{\rho})^2 + W_{311}(\vec{H} \cdot \vec{H})(\vec{H} \cdot \vec{\rho}) \notag \\ & + W_{400}(\vec{H} \cdot \vec{H})^2 + \cdots \end{align}

この展開式において\(n=i+j\)をその項の”次数”と呼ぶ。前回は\(n=0, 2\)次の項について紹介した。今回はザイデル収差と密接に関連する\(n=4\)（４次）の項を扱う。波面収差関数の\(n=4\)の項には\(W_{400}, W_{040}, W_{222}, W_{220}, W_{311}, W_{131}\)が含まれる。前回と同様に、\(\vec{\rho}\)の依存性を持たない\(W_{400}\)の項は位相のオフセットに相当する項（特に視野中心から距離の４乗に比例して大きくなるオフセット）であり、像面上で収差を作らないため無視する。今回はスペースの都合上、\(W_{040}, W_{222}, W_{220}\)に絞って解説をする。

\(W_{040}\)の項

この項は次のように式変形できる。

$$W_{040}(\vec{\rho} \cdot \vec{\rho})^2 = W_{040}\rho^4\tag{1}$$

つまり、図１の左に示すように波面の４次関数成分を表すものである。理想球面と比較した場合、瞳の中心付近では波面の傾斜は緩やかであるが、波面周縁部に近づくにつれて傾斜が大きくなり、やがて傾斜は逆転する。したがって波面中心の光線（波面）の結像点が主光線のそれよりも遠くになるが、波面周縁部の光線（波面）の結像点は主光線のそれより近くなる（\(W_{040}\)の符号が逆転した場合は逆センスになる）。すなわち波面の４次関数成分は、瞳中心を中心とした輪帯ごとに結像位置を変動させる。この変化は視野\(\vec{H}\)に依存しない(式（１）および図１右)。この項はザイデル収差における球面収差に対応する。

 

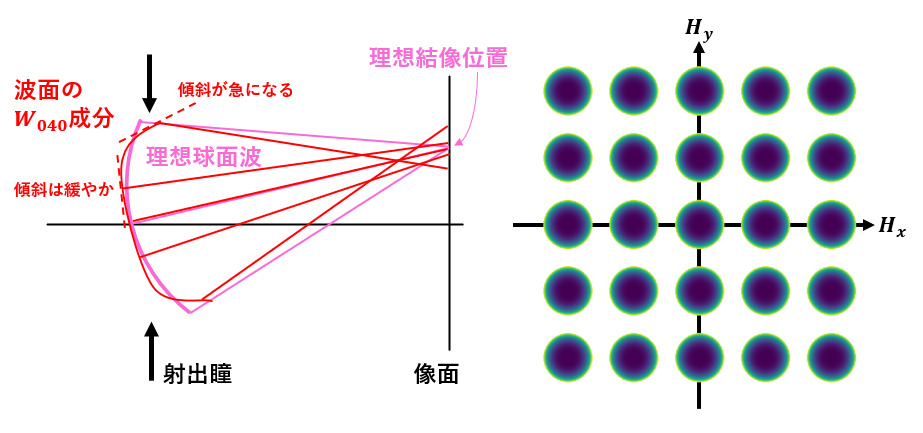
図１：\(W_{040}\)の波面収差の断面図（左）と視野の各点での\(W_{040}\)の形状をカラーマップでプロットしたもの（右）

 

\(W_{222}\)の項：

この項は次のように式変形できる。

$$ W_{222}(\vec{H} \cdot \vec{\rho})^2 = W_{222}H^2 \rho^2 cos^2 \theta \tag{2}$$

ここで、\(H=|\vec{H}|\)であり、\(\theta\)は\(\vec{H}\)と\(\vec{\rho}\)がなす角である。\(\vec{H}\)と光軸を含む面（メリディオナル面）とそれに直交する面（サジタル面）は、それぞれ\(\theta=0^{\circ}\)（\(180^{\circ}\)）、\(\theta=90^{\circ}\)（\(270^{\circ}\)）で定義され、各面内の波面はそれぞれ次のようになる。

\begin{equation} W_{222}(\vec{H} \cdot \vec{\rho})^2 = \begin{cases} W_{222}H^2 \rho^2 & (メリディオナル面上) \\
0 & (サジタル面上) \end{cases}\tag{3} \end{equation}

つまり、\(W_{222}\)の項は波面の放物柱形状（図２参照）の成分を表すものである。図３の場合では、メリディオナル面内の波面が理想結像位置よりも遠くに結像する様子を示している（\(W_{222}\)の符号が逆転した場合は、逆に遠くに結像する）。一方でサジタル面上の波面は理想結像する。見方を変えれば、波面の放物柱形状の成分はメリディオナル面とサジタル面内でパワーが異なっているとも解釈できる。また、式（２）よりこのパワーの変化は視野の２乗に比例する（図３右）。したがって\(W_{222}\)の項はザイデル収差の非点収差に対応する。

 

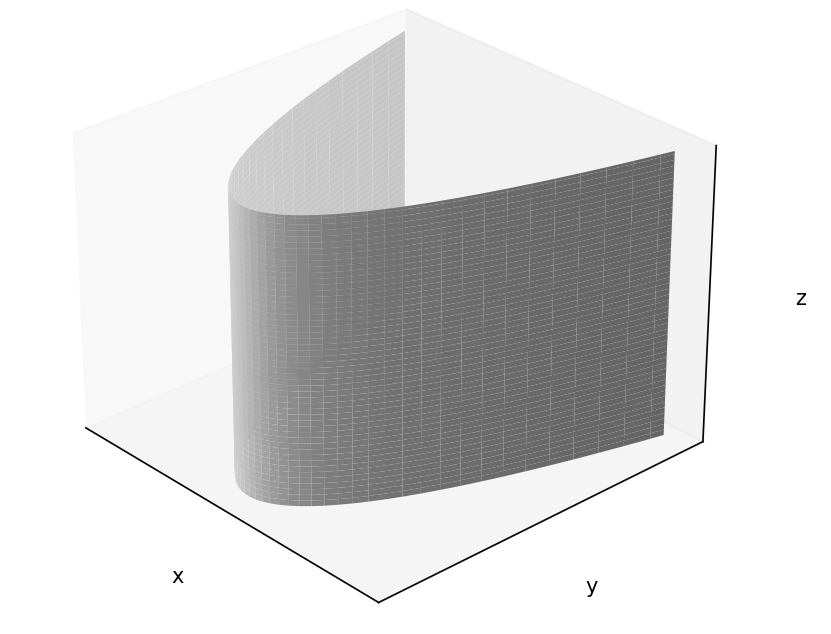
図２：放物柱形状

 

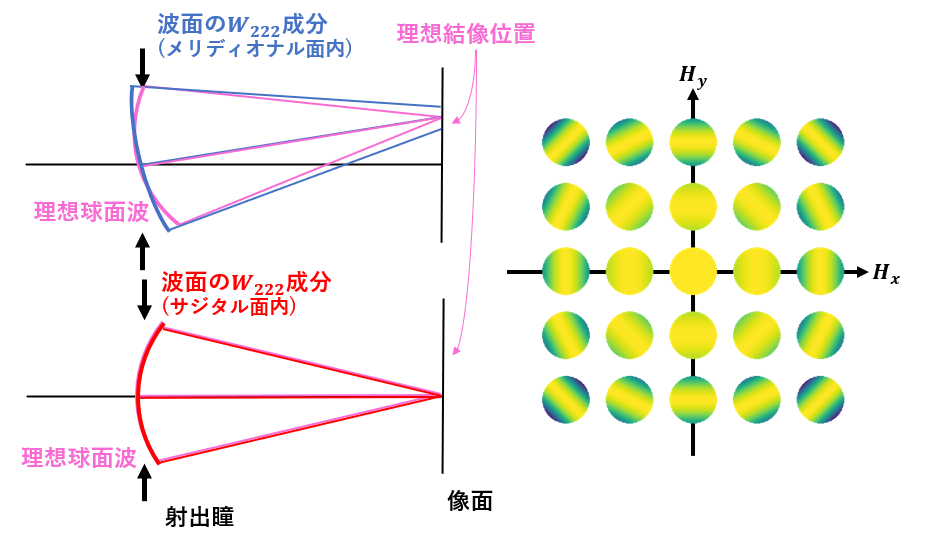
図３：\(W_{222}\)の波面収差の断面図（左）と視野の各点での\(W_{222}\)の形状をカラーマップでプロットしたもの（右）

 

\(W_{220}\)の項：

この項は次のような式で表される。

$$(W_{220}の項)=W_{220}(\vec{H} \cdot \vec{H})(\vec{\rho} \cdot \vec{\rho})\tag{4}$$

\(\vec{H}\)を固定したときは\((\vec{\rho} \cdot \vec{\rho})\)の部分のみが残るが、\(W_{020}\)と同じである。したがって、波面の放物面成分、つまりはデフォーカスを表している。\(W_{020}\)のとの違いは視野依存性にある。\(W_{020}\)の項は視野一様なデフォーカスを生成するが、\(W_{220}\)の項は視野の２乗に比例したデフォーカスに対応する（図４右）。言い換える視野が大きくなるにつれてデフォーカスが大きくなる、ということである。これはまさにザイデル収差の像面湾曲に対応する。

 

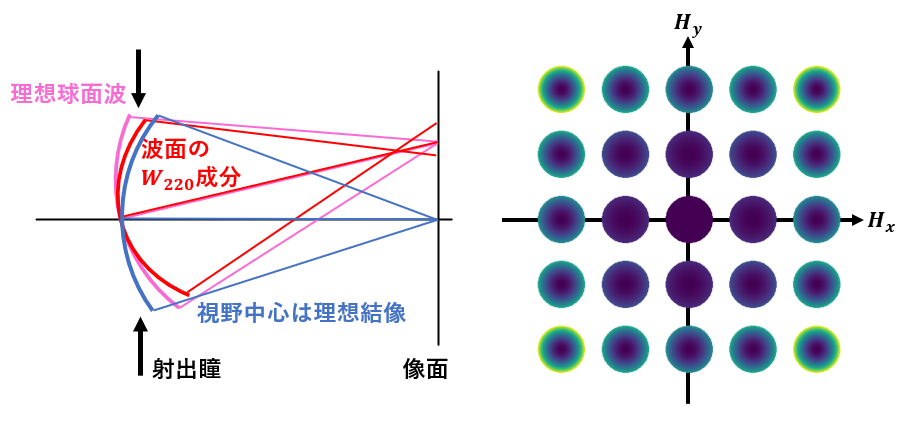
図４：\(W_{220}\)の波面収差の断面図（左）と視野の各点での\(W_{220}\)の形状をカラーマップでプロットしたもの（右）

 

ここまでの説明から予想できるように、残る\(W_{311}, W_{131}\)は歪曲とコマ収差に対応する項である。それらについては次回以降に紹介する。