波動光学を理解する（２）

復習はこちらから：
波動光学を理解する（１）：光の取り扱い方　

古典電磁気学が確立するより以前の1600年代に、ホイヘンス(Huygens)は光の性質(直進・屈折・反射・回折・干渉)を説明するために、光は「波動」であるという仮説を立てた。この仮説では図１のように光を波動と捉え、ある瞬間の光の波面の各点から素元波と呼ばれる球面波の２次波が放出され、それらが互いに重なり合って形成される新たな包絡線が次の波面となると考える。この考え方は「ホイヘンスの原理」と呼ばれる。ホイヘンスの原理を用いると、少ない仮定で光の性質を説明することが出来る。

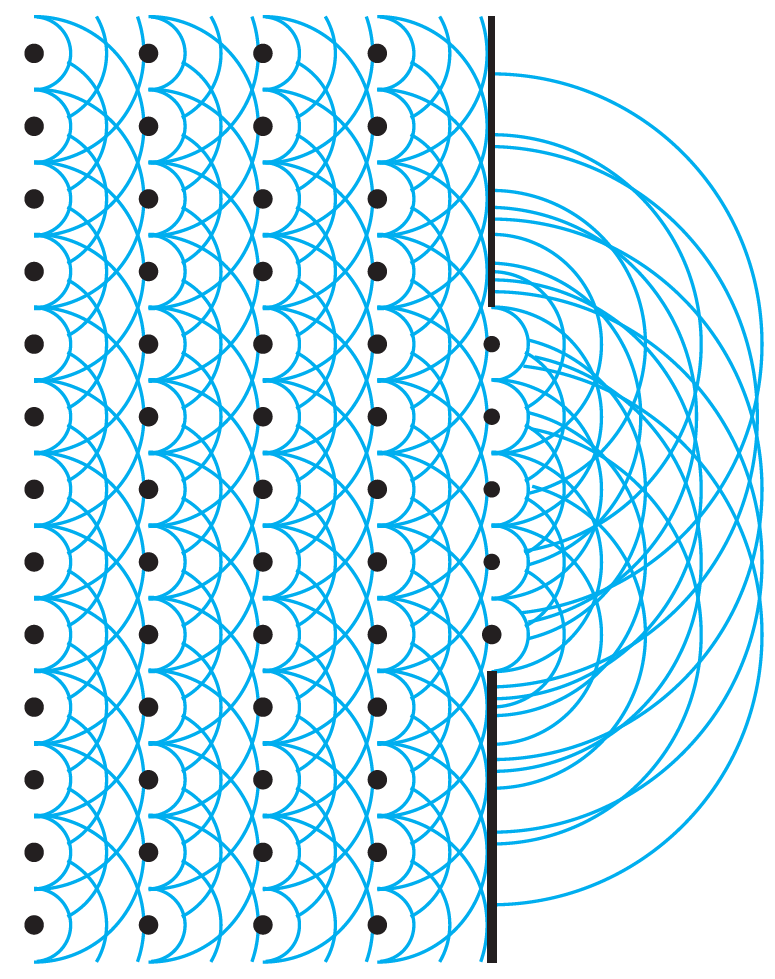
図１：ホイヘンスの原理

しかしながら、当時はニュートン(Newton)が光の粒子説を提唱していたこともあり、ホイヘンスのこのアイディアは見過ごされることとなる。しかしながら、それから約200年後の1807年に、ヤング(Young)が有名な二重スリットの実験を実施。実験において光の干渉縞が確認されたことで、光が波動であることが確定すると、ホイヘンスのアイディアが見直されることになった。特にフレネル(Fresnel)は、次の条件を満たすようにホイヘンスの原理を数学的に定式化した：

第一の条件は波の性質として自然なものであり、第二の条件は実際の光の強度変化から自然なものである。

特に、図２のように左側から平面波によって照らされる開口（\(z=0\)に位置し開口上の電場の複素振幅は\(E(x’,y’,0)\)）があった場合に、その右側の位置\((x,y,z)\)の位置に出来る光の電場の複素振幅は次の「ホイヘンス-フレネル回折積分」で与えられる：

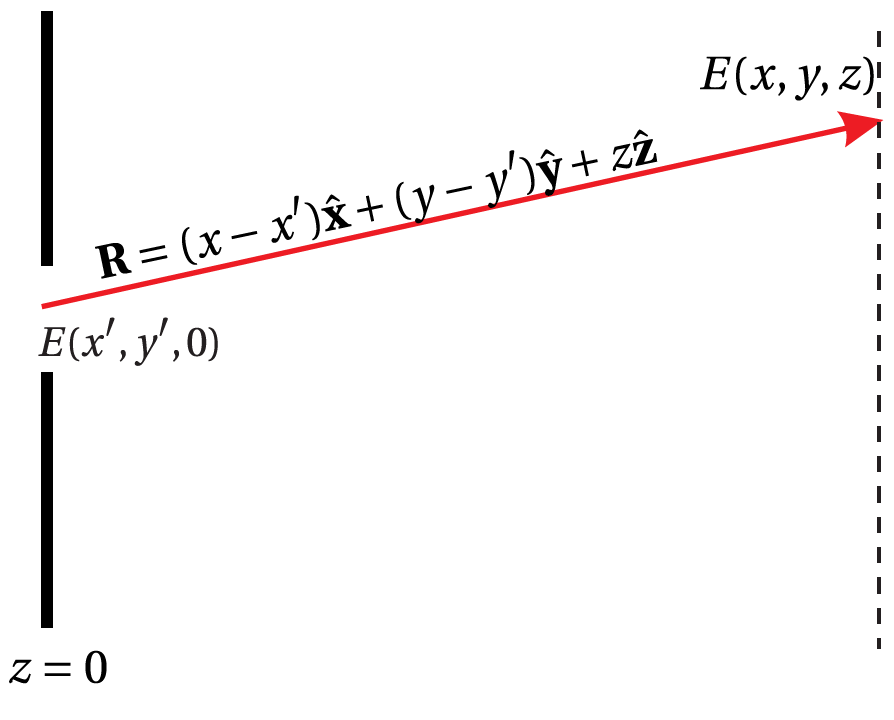
図２：ホイヘンス-フレネル回折積分

ホイヘンス-フレネル回折積分：
\begin{align}
E(x,y,z) = – \frac{i}{\lambda} \iint_\text{開口} E(x’,y’,0) \frac{e^{ikR}}{R} dx’ dy’
\end{align}
ただし、
\begin{align}
R = \sqrt{(x-x’)^2+(y-y’)^2+z^2}
\end{align}

これは開口上の全ての点からの２次波の寄与を積分によって足し上げている。ただし、積分の前の係数\(-\frac{i}{\lambda}\)の意味は不明確である。\(1/\lambda\)は次元を合わせるためと捉えることは出来るが、\(-i\)と位相をずらす意味は明らかでない。実はホイヘンス-フレネル回折積分の段階ではこの係数の根拠は分からず、実験と合うようにしているに過ぎない。今後に解説する「フレネル-キルヒホッフ(Kirchhoff)回折の式」によってこの係数が正しいことが分かる。

このホイヘンス-フレネル回折積分には他にも問題がある。それは、ホイヘンス-フレネル回折積分に従うと、２次波は波面の各点から全方向に向かって球対称に放出されるため、波が進行方向だけではなく、逆方向(波源の方向)にも進行してしまうことである。現実では波は逆方向には進行しないため、この点に関してはホイヘンス-フレネル回折積分は現実と整合しない。この点に関してもフレネル-キルヒホッフ回折の式では２次波の放出強度が等方ではなくなる(進行方向に強く、波源の方向に弱い)ために解消される。