
以前の記事で紹介したフィルターを理解するには、波の反射・干渉などの現象を理解する必要がある。今回は波の反射における境界条件について考えよう。
波の反射現象を考えるための境界条件に、”固定端”と”自由端”というものがある。
まずはロープのようなものの一端から波が発生する状況を考えよう。波はロープを伝わりもう一方の端(他端)に到達した後、再びロープを伝って戻ってくる(反射される)。反射された波(反射波)は、他端を固定した場合と固定しない場合とで異なる。他端が”固定されている”場合は、他端での合成波の振幅は常にゼロであるので、反射波の位相は入射波に対して常に半位相ずれていなければならない。これが固定端条件である。一方で、固定されていない場合は、反射波と入射波の位相は同じになる。これが自由端条件である。
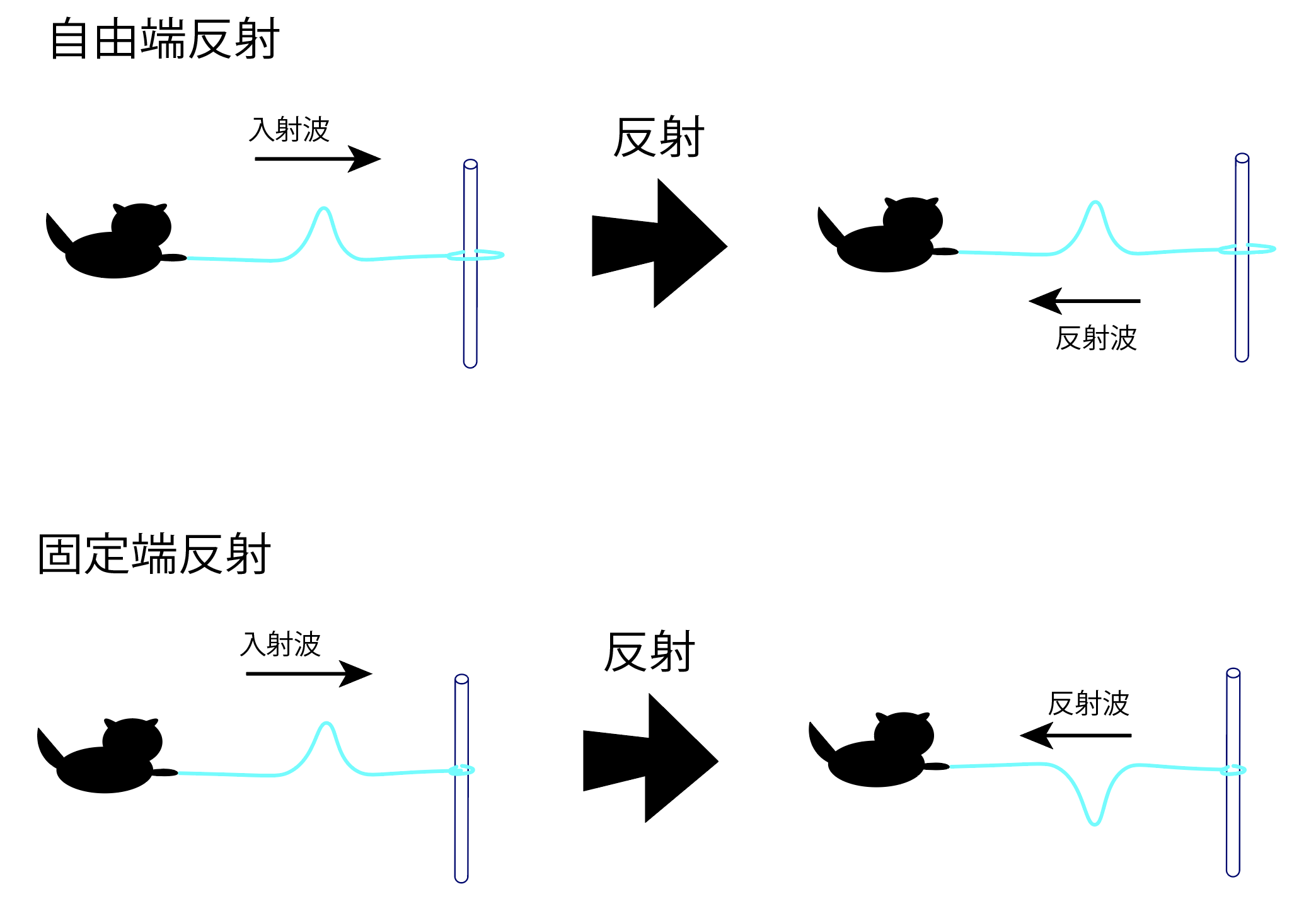
図1:ロープの自由端・固定端反射
この2つの反射波の境界条件は、光の反射にも登場する。入射光が通過する媒質が界面を作る媒質の屈折率よりも低い場合、すなわち屈折率の低い媒質から高い媒質へと入射する場合は、反射光は固定端条件で反射する。逆の場合は自由端条件になる。さきほどのロープの例の場合は、端が明確に固定されている(振幅はゼロになる)ので固定端条件になるのは理解しやすい。ところが、光の場合は一般に界面での振幅はゼロにはなっていないはずである。なのに、固定端条件が発生する(その結果、位相がジャンプする)のはなんだか不思議である。今回はその理由については考えてみよう。
光の反射現象において、振幅反射率の式がある。入射側と透過側の媒質の屈折率の大小によって、固定端条件になったり自由端条件になったりするのはこの式を見れば一目瞭然である。
$$r = \frac{(n_{i} – n_{t})}{(n_{i} + n_{t})}$$
入射側の屈折率\(n_{i}\)が透過側の屈折率\(n_{t}\)よりも小さい場合は、振幅反射率\(r\)は負の値になる。振幅が負になるということは、位相が半波長だけずれていると言い換えてもよいわけで、たしかに位相がジャンプしている。多くの教科書はこの式を以て”以上、説明終わり”である。この式は、マクスウェル方程式を端緒にして、界面における電場(電束密度)と磁場(磁束密度)の境界条件を考えることによって得られるわけだが、到達するまでの複雑な式変形によって、物理的な意味を理解することが困難になっている(と思う)。聡明な読者であれば「そんなことはない」と言われるかもしれないが、暗愚な筆者にとっては少なくともそうである。
そこで難しいマクスウェル方程式から始めるのでなく、波の一般論からこの問題にアタックしたいと思う。この試みは次回にお届けしよう。

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。