
Computer Generated Hologram(計算機生成ホログラム、CGH)は、光の回折・干渉の効果を使い、任意の方向に光を飛ばす(波面を作る)ことが可能な光学素子である。今回はCGHの回折次数について解説する。
CGHを理解する:古典的回折格子の原理(2)で紹介した回折格子の式は以下の式であった。
$$ d \sin{\theta} = m \lambda \tag{1} $$
(1)に出てくる変数はそれぞれ、回折格子の溝間隔\(d\)、波長\(\lambda\)、回折次数\(m\)、回折角\(\theta\)を表す。またCGHを理解する:回折角の記事にて、\(\lambda=0.633 \mu m\)、\(m=1\)の場合の例として、回折角\(\theta\)と回折格子の溝間隔\(d\)の関係とをグラフで示した。CGHを製作する際のレーザーマスクレスリソグラフィーのPSFサイズの制限から、溝間隔は概ね\(d\sim2 \mu m\)が下限値であるため、グラフから最大回折角は\(\theta\sim18.5^{\circ}\)程度になることが読み取れた。
その際にも言及したが、CGHのアプリケーションにおいて回折角を\(\theta\sim18.5^{\circ}\)よりも大きくしたい場合はどうしたらよいのだろうか?その1つの方法が「高次回折光(\(m = \pm2, \pm3, \cdots\))を用いる」というものだ。CGHを理解する:古典的回折格子の原理(2)でも説明したが、振幅変調バイナリ型CGHは0次光、\(\pm\)1次、\(\pm\)2次、\(\pm\)3次、\(\cdots\)と多数の次数の波面を生成する。通常大きな回折角が不要な場合は、回折効率などの観点から\(\pm\)1次光を使用することが多いが、大きな回折角が必要な場合は\(\pm\)2次光を使用することもある。
図1にCGHの各開口から射出される球面波が干渉し、1次光と2次光を生成する様子を図示した。2次光は1次光に対してより大きく曲がって(大きな回折角を持って)いることが見てわかるだろう。図2は(1)式で波長\(\lambda = 0.633 \mu m\)とし、回折次数を変えた場合に回折角\(\theta\)とそれに対応する溝間隔\(d\)をグラフにしたものである。同じ溝間隔\(d\)でも、回折次数を\(m=\pm2\)もしくは\(m=\pm3\)とすると、\(m=\pm1\)に対して大きく曲がることがグラフから読み取れるだろう。具体的に計算してみると、波長\(\lambda = 0.633 \mu m\)において、レーザースクレスリソグラフィーによる描画限界である\(d \sim2 \mu m\)の場合で、\(\pm\)1次光(\(m=\pm1\))の回折角は\(\theta\sim18.5^{\circ}\)であるのに対し、\(\pm\)2次光(\(m=\pm2\))では回折角が\(\theta\sim39.3^{\circ}\)となり、さらに\(\pm\)3次光(\(m=\pm3\))では回折角が\(\theta\sim71.7^{\circ}\)となる。このように高い回折次数を使用することで、より大きな回折角を持つビームを得ることができるのだ。
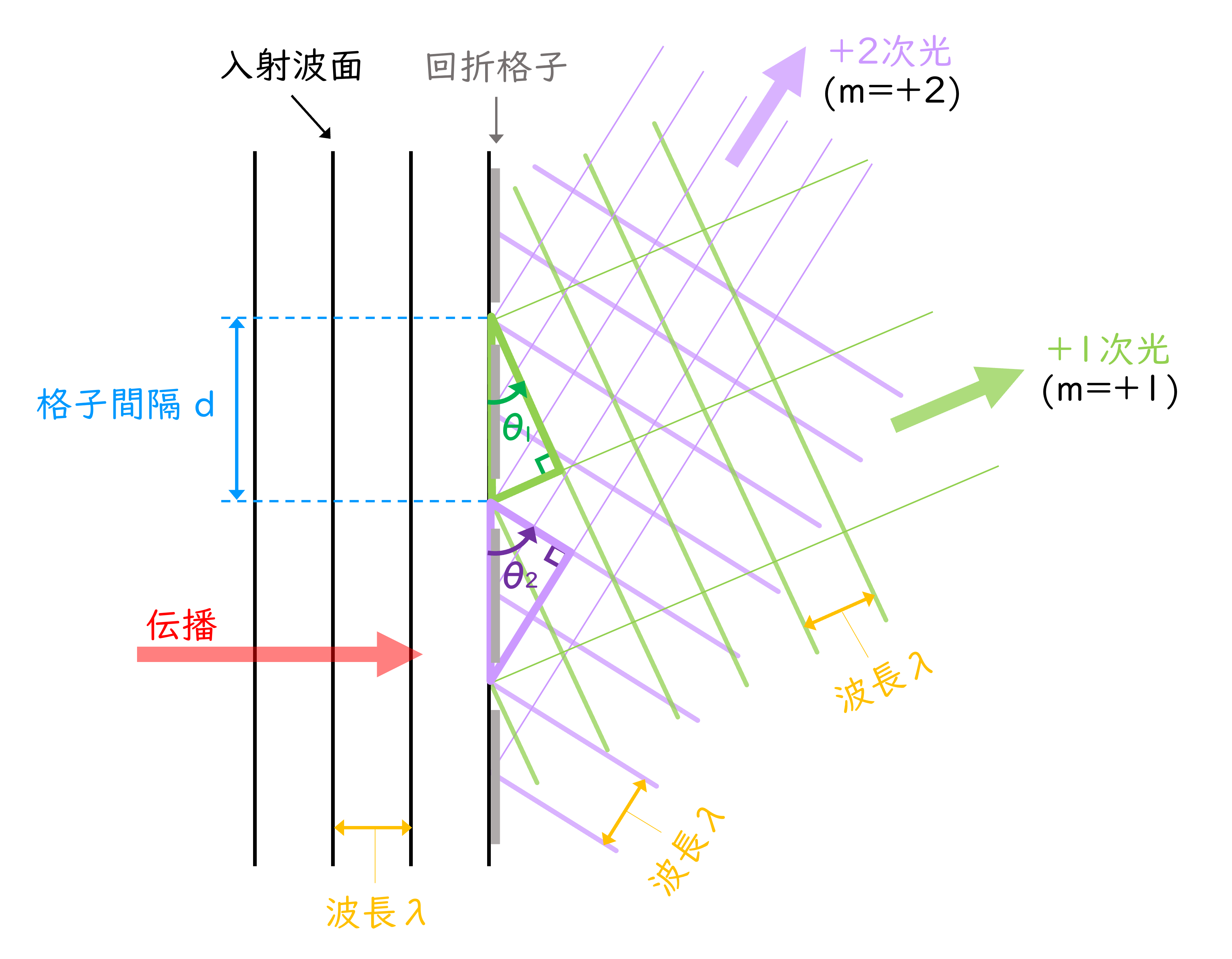
図1:1次回折光と2次回折光

図2:回折次数と回折角
(波長\(\lambda=0.633\mu m\)の例)
しかしながら、高次回折光を使用した場合、次数が低い回折光に比べて回折効率が低下し、目的の波面の光が暗くなってしまうため、実際には使用しにくい場合がある。回折効率については次回以降の記事に譲ることとしよう。

大学院在学中は素粒子物理学を専攻。趣味の天体写真も物理理論に裏付けられた解析方法を行っており、 アマチュア天文家の間で蔓延している都市伝説は一切信じない。赤道儀マニアでアマチュア天文機器にやたら詳しい。 計算機ホログラム(CGH)や干渉計などの高度な物理計算を軽々とこなす。 光学・物理学に関連する原理や数学的理解に関する記事を担当。