
上の画像は一見すると単一画像のように見えるが、右上や中央やや上部分に点線上の軌跡が見られる。これは恒星の動きとは異なるもの(人工衛星や飛行機)が星々の間を移動していく様子を捉えたものに他ならないのだが、この軌跡が点線になって見えるということは、複数枚の天体画像を撮影しそれらを重ね合わせたという間接的な証拠である。デジタルカメラが普及した後の天体画像は、長時間露光を行う「一発撮り」ではなく、短時間露光の画像を重ね合わせたものが一般的なのだが、そのメリットや背景について説明しよう。
この画像処理のことをアマチュア天文家の間では「コンポジット」と呼ぶことが多い。コンポジットは「複合・合成」といった意味の英語の”composite”をそのまま読んだものである。よくゲームや映画などの音楽を作曲する方のことを「コンポーザー」というが、これは様々な音を複合して1つの曲にするという意図が込められた言葉だと言える。天文画像のコンポジットは、同じ天体を撮影した複数の画像を位置合わせをした後に加算もしくは加算平均して一枚の画像を作ることである。ちなみに研究者はコンポジットという言葉はあまりなじみがなく、「スタック(stack、積み重ね)」「シフト&アド(shift & add)」と呼ぶことが多い。
コンポジットの効果はずばり「S/Nの向上」である。S/Nは「ノイズ」と「S/N(SN比)」の違いなどの記事でも取り上げたとおり、真の値とノイズとの比であるが、コンポジットによりS/Nがどう変化するのかを図1に示した。このシミュレーションでは、簡単のため一様な明るさのものをn枚撮影した画像を、加算平均にてコンポジットしている。各直方体の高さがそれぞれのピクセルのカウント値(CCD/CMOSの各ピクセルに溜まった電子の量)を表す。
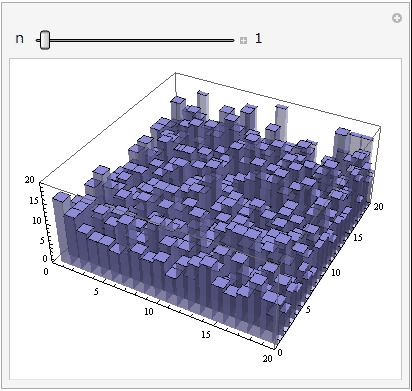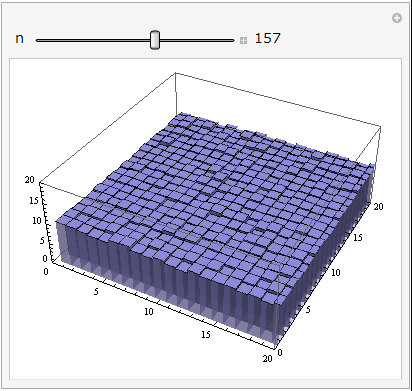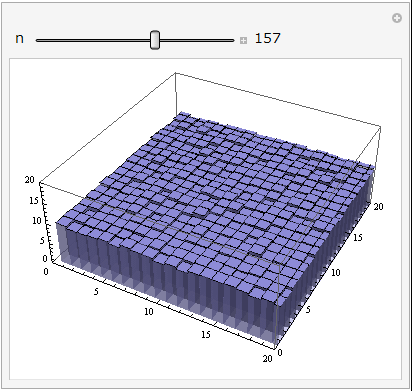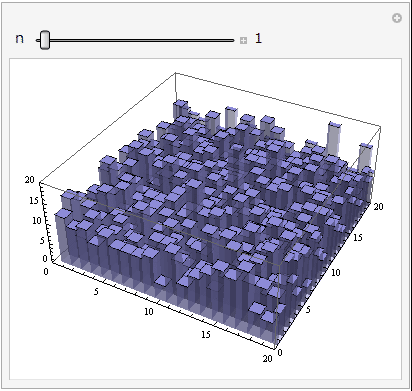
図1:一様な明るさのものをn枚撮影した画像に対し加算平均にてコンポジットした場合のシミュレーション。
図1をよく見ると、コンポジット枚数nが増えるにつれて画像がどんどん滑らかになっていくのが分かる。加算平均なので、シグナルSの大きさはコンポジットをしても変わらないのだが、ノイズNの大きさがどんどん小さくなり、結果としてコンポジット後の画像のS/Nは向上して滑らかになる。天体画像の主要なノイズ源にショットノイズがあるが、ショットノイズの場合はシグナルSとノイズNの間に\(N\propto \sqrt{S}\)の関係があるため、\(S/N \propto \sqrt{S}\)となる。これはつまりS/Nは露出時間のルートもしくは撮影枚数のルートに比例して良くなっていくということを意味する。(ショットノイズについて復習されたい方はフォトンノイズ(ショットノイズ)とは何か?からどうぞ。)
\begin{align*} S/N & \propto \sqrt{\text{Time}}\\ & \propto \sqrt{\text{number}} \tag{1}\end{align*}
(1)をグラフにしたものが図2である。例えばコンポジット枚数を2枚から8枚に増やすと、S/Nは\(\sqrt{\frac{8}{2}}=2\)倍に向上するが、64枚を70枚に増やした場合、S/Nは\(\sqrt{\frac{70}{64}}=1.05\)倍にしかならない。同じ「6枚増やす」という操作でも、画像に対する(S/Nに対する)寄与具合が異なるのだ。
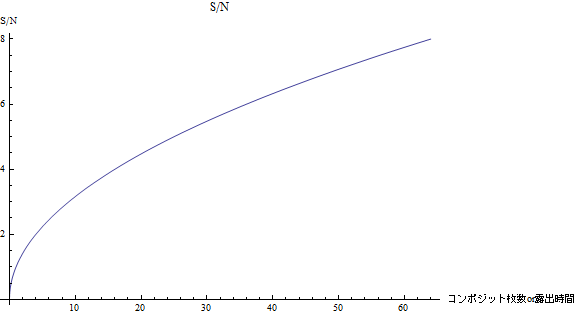
図2:コンポジット枚数とS/Nの関係
たまに聞く話として「ダークのコンポジットでは64枚以上増やしてもあまり関係ない」というものがあるが、これはこのような事情を考えての発言だと理解出来る。(もちろんコンポジット枚数を増やせば確実にS/Nは向上するのだが、撮影の労力と効果を考えると64枚程度で十分?という話なのだと思われる。例えば64枚からS/Nを2倍高めようと思うと、\(64\times4=256\)枚撮影する必要がある。)
ここでは加算平均コンポジットの場合で考えたが、加算コンポジットの場合でもS/Nは全く同じように向上する。どうしてかな?と思われた方はぜひノイズを計算する(1)のシリーズを読んで頂きたい。

大学院在学中は素粒子物理学を専攻。趣味の天体写真も物理理論に裏付けられた解析方法を行っており、 アマチュア天文家の間で蔓延している都市伝説は一切信じない。赤道儀マニアでアマチュア天文機器にやたら詳しい。 計算機ホログラム(CGH)や干渉計などの高度な物理計算を軽々とこなす。 光学・物理学に関連する原理や数学的理解に関する記事を担当。