CGHを理解する：回折角

CGHを理解する：古典的回折格子の原理（１）およびCGHを理解する：古典的回折格子の原理（２）でも取り扱った「回折格子の式」は以下である。

$$ d \sin{\theta} = m \lambda \tag{1} $$

ここで、\(d\)は回折格子の溝間隔、\(\theta\)は回折角、\(m\)は回折次数、\(\lambda\)は光の波長を表すのであった。例として、\(\lambda=0.633 \mu m, m=1\)の場合を考えると、回折格子の式は以下のようになる：

$$ d[\mu m] \times \sin{\theta} = 0.633 \mu m \tag{2} $$

（２）式を満たす回折角\(\theta\)と溝間隔dの関係をグラフに表したものが図１である。この図から、回折角\(\theta\)を大きくするには、回折格子の溝間隔\(d\)を小さくする必要があることが分かる。

 

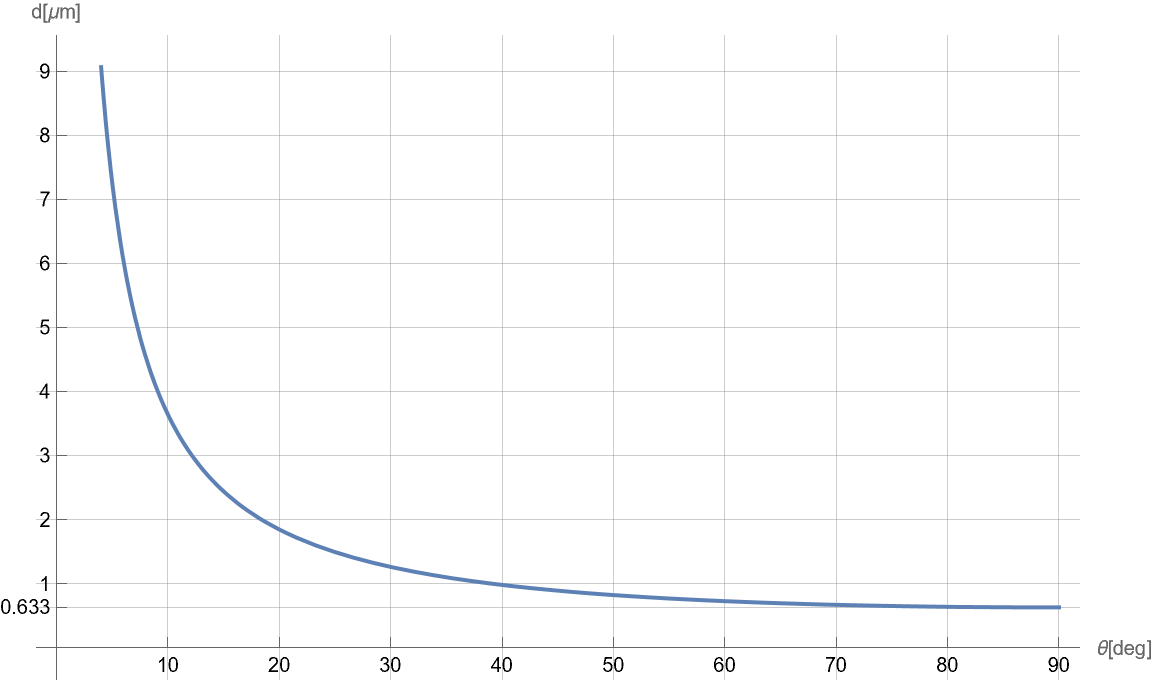
図1：（２）式を満たす回折角\(\theta\)と溝間隔\(d\) の関係

 

さらに図１からは、
(1)回折角\(\theta\)を\(0^{\circ}\)に近づけると、溝間隔\(d\)は無限大に発散する
(2)回折角\(\theta\)を\(90^{\circ}\)に近づけると、溝間隔\(d\)は波長\(\lambda=0.633\mu m\)に収束する
ことも見て取れる。

(1)にある「溝間隔\(d\)が無限大」というのは、無限に広い開口があり、隣の開口までの距離が無限大になっている状況と考えることができる。この場合は回折格子が存在しない状況と同じであるため、光が曲がることなく直進し、回折角\(\theta=0^{\circ}\)となることが直感的に理解できる。(2)の「溝間隔\(d\)が波長\(\lambda\)と同じの場合」というのは、回折格子を通過後の光が\(90^{\circ}\)真横に曲がったとき、各開口を通過した波面がちょうど強め合う干渉を起こす状況に対応している。前回のCGHを理解する：古典的回折格子の原理（２）の図2および数式（２）の両方を見ながら、図によるイメージと数式を対応させることができると、より理解が深まるだろう。

CGHは通常、レーザー描画マスクレスリソグラフィーによって作成される。描画レーザーのPSFは回折限界スポットサイズであり、典型的な描画機では\(\sim1\mu m\)の大きさを持つ。そのため、レーザーによって作られる開口部の幅は\(\sim1\mu m\)が下限値となり、CGHの格子間隔（＝古典的回折格子の溝間隔）\(d\)はその2倍の\(\sim2\mu m\)が下限値となる。例えば干渉計測定などでよく使われるHe-Neレーザーの波長\(\lambda=0.633\mu m\)の場合、図１から回折角\(\theta\sim18.5^{\circ}\)が最大であることが見て取れる。

実際のCGHのアプリケーションでは、多くの場合はこの回折角があれば十分であるが、より大きな回折角が必要となる場合も存在する。例えば非球面量の非常に大きな自由曲面ミラーをレーザー干渉計によって測定する場合や、アライメント用に特殊なビームが必要となる場合などは大きな回折角が必要になることがある。では、そのような場合にCGHで大きな回折角を実現するにはどうすれば良いのだろうか？この点は次回以降に譲ることにしよう。