CGHを理解する：古典的回折格子の原理（２）

各開口からの波面が揃い、重なっている部分が強め合う干渉を起こすと、複数の波面（0次光、\(\pm1\)次光）が生成される（図１）。0次光の波面は、左から入射した波面が回折格子の遮蔽部によって一度は途切れるが、伝搬して広がって行くにつれて再度連続的に重ね合わさったと考えることで、直感的に理解することが出来るだろう。\(\pm1\)次光の波面については、途切れた波面が伝搬しながら再度重ね合わせが起こる際に、元々の波面ではなく、1波長分だけ進んだ/遅れた波面と重ね合わさることで形成されたと理解することが出来る。すなわち、開口を通過した波面の重ね合わせの際に、ある種の「ボタンの掛け違い」のような現象が起こることで、\(\pm1\)次光のような角度を持った波面が形成されるわけだ。このように考えることで、回折次数と波面の関係について直感的にも理解ができるだろう。

 

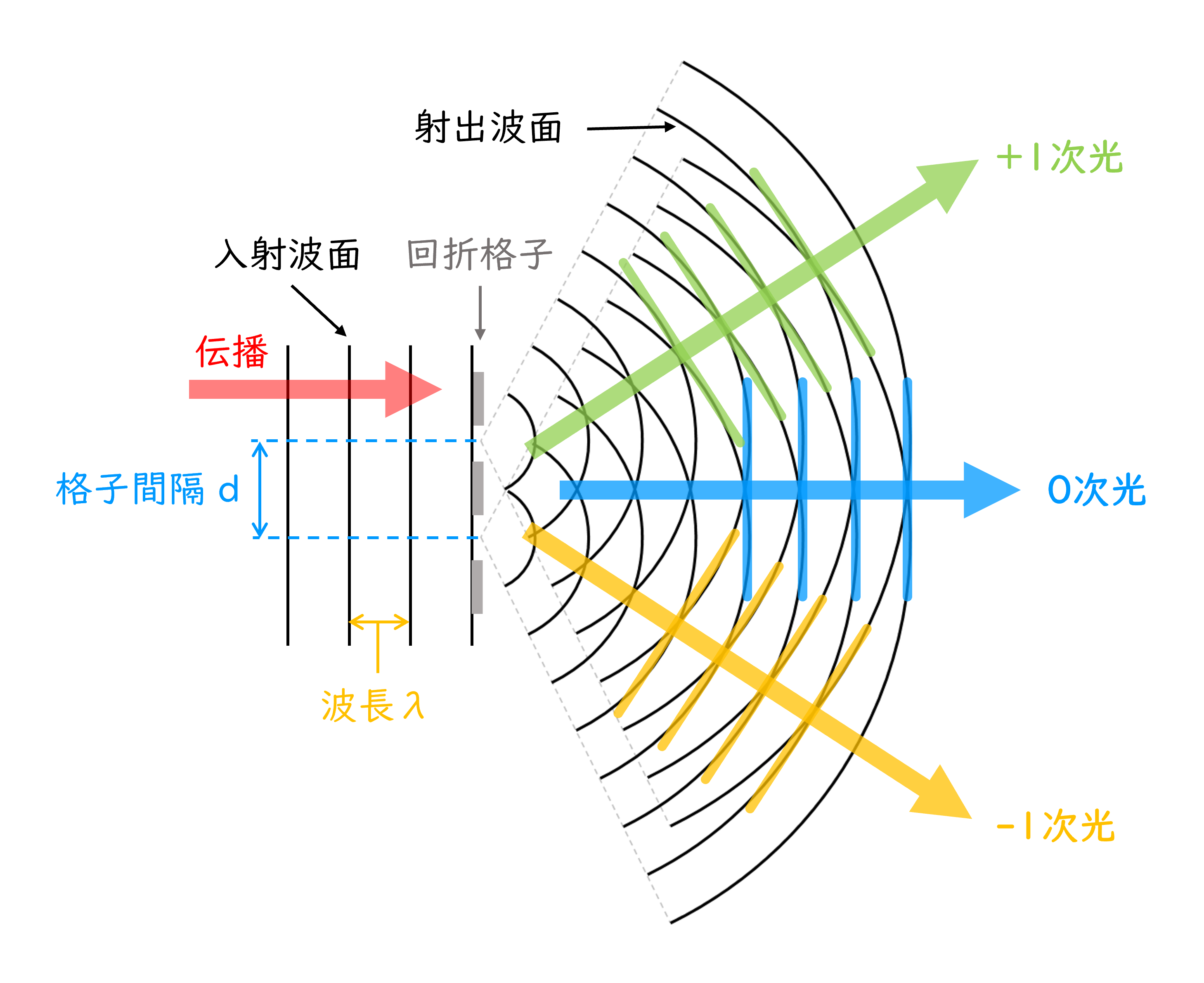
図１：回折格子通過後に形成される光の波面。
光の干渉に伴い、直進する0次光だけでなく、入射光に対して角度をもった波（例：\(\pm\)1次光）が現れる。

 

　

なお図1では3つの波面（0次光、\(\pm1\)次光）のみを例として描いているが、これ以外にも２波長分ずれた波、3波長分ずれた波との重ね合わせも考えることができ、\(\pm\)2次、\(\pm\)3次、\(\cdots\)の波面も生成される。高次の波面が図1中のどこに描かれるのか、ぜひ考えてみてもらいたい。このようにして、古典的な回折格子は入射光から複数の次数の波面を生成し、それぞれ異なる方向に伝搬させることが出来るのだ。

最後にこの関係を数式で表現してみよう。回折格子の溝間隔\(d\)、入射光の波長\(\lambda\)、回折光の次数\(m\)、回折角\(\theta\)に対し、図2中の橙色の直角三角形に注目すると、三角比の定義から次の関係式が成り立っていることが分かる。

$$ d \sin{\theta} = \lambda \tag{1} $$

 

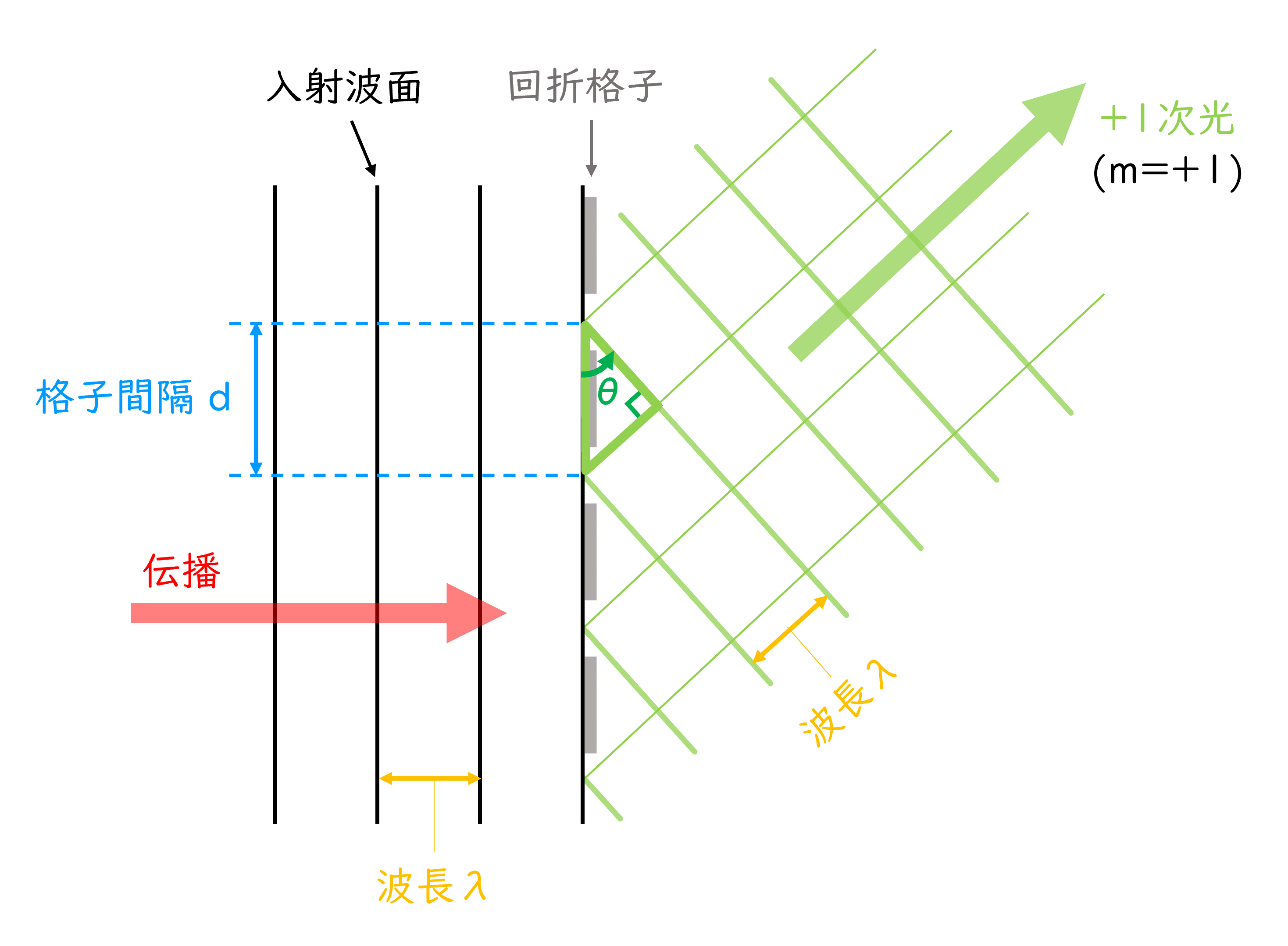
図２：図１のうち、＋１次光の波面および波の進行方向のみを表記したもの。
回折格子の溝間隔\(d\)、入射光の波長\(\lambda\)、回折光の次数\(m\)、回折角\(\theta\)も合わせて記載。

 

　

（1）式は\(m=+1\)に対してのみ成り立つ関係式だが、それ以外の回折次数\(m\)に対しても成り立つため、以下のように表現できる。

$$ d \sin{\theta} = m \lambda \tag{2} $$

これがまさに、前回の記事の冒頭で紹介した「回折格子の式」そのものである。なお、今回は入射光が回折格子に対して垂直入射する場合を考えたが、入射角をもつ場合は、(2)式の左辺の\(\sin{\theta}\)の部分を変えなくてはいけない。この詳細については別の機会に譲ることにしよう。

　
回折格子の式は非常に重要な式であり、この式から各変数（\(d\)、\(\lambda\)など）を変えた場合の古典的な回折格子の振る舞いを理解することが出来る。例えば、格子の溝間隔\(d\)を小さくすると、回折角\(\theta\)が大きくなり、光が大きく曲がるようになることが分かるだろう。同様に波長\(\lambda\)を短くしたり、回折次数の絶対値\(\lvert
m \rvert\)を大きくすることでも光の曲がりが大きくなることが分かる。また、この式はCGHの設計においても重要な役割を果たす。格子の溝間隔\(d\)を変えることで回折角\(\theta\)を変えることができるため、回折格子の溝間隔\(d\)を場所によって変化させることで、回折格子上の場所毎に光を異なる角度に曲げることが可能になる。この原理を用い、CGHでは格子の溝間隔\(d\)を精密にコントロールすることで任意の波面を作り出しているのだ。