
Computer Generated Hologram(計算機生成ホログラム、CGH)は、光の回折・干渉の効果を使い、任意の方向に光を飛ばす(波面を作る)ことが可能な光学素子である。「CGHを理解する」のシリーズでは、CGHの仕組みを理解するために、同じく回折・干渉の効果によって光を曲げる(波面を変える)「回折格子」の原理と「回折格子の式」と呼ばれる重要な関係式について説明する。
高校物理の教科書などで取り扱われる「回折格子の式」は、以下のようなものである。
$$ d \sin{\theta} = m \lambda \tag{1} $$
ここでdは回折格子の溝間隔、\(\theta\)は回折によって光が曲がる角度(回折角)、mは整数(後述、回折次数)、\(\lambda\)は光の波長である。教科書では「この式の条件を満たす場合、回折格子を通った光が強め合う」と説明がされるが、本記事ではこの式の背景を解説する。
今回考える回折格子は、振幅変調型回折格子というタイプの回折格子である。ここでは「古典的回折格子」と呼ぶが、任意の方向に光を曲げることができる機能はCGHと同じであるため、”最も簡単なCGH”とも言えるだろう。図1に古典的な回折格子に左から波長\(\lambda\)の平行ビーム(平面波)を垂直に入射させた模式図を示す。今回は簡単のため平面波が回折格子に垂直入射する場合を考えるが、ここから導かれる考え方自体はそれ以外の場合にも適応が可能である。古典的な回折格子は、光を通す開口部と通さない遮蔽部が正確な周期で繰り返す構造を持つ。隣接する開口間の距離は「格子間隔」(あるいは溝間隔)と呼ばれ、(1)式の”d”である。
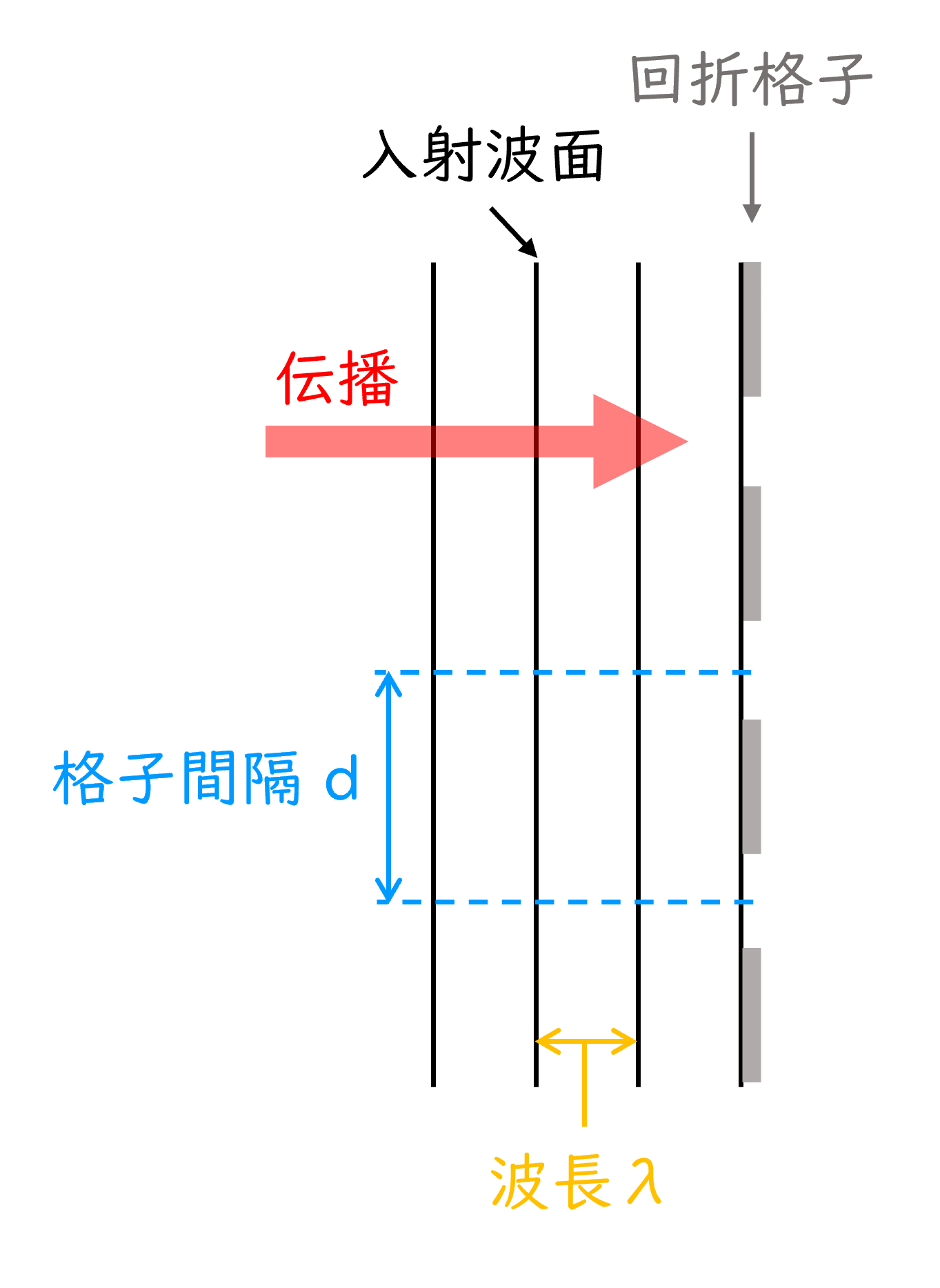
図1:古典的な回折格子とそれに垂直入射する平行ビーム(平面波)
最終的に考えたいことは、この回折格子を通過した光の振る舞いであるが、まずはその手がかりに、一つの開口部を通った光の振る舞いを見てみよう(図2)。回折格子に左から垂直入射した波長\(\lambda\)の平行ビーム(平面波)の一部は遮蔽部で遮られるため、光は開口部でのみ右側へと進む。開口部を通過した光は回折によって壁の裏側へと回り込むため、結果的に一つの開口を通過した光の波面は開口の位置を中心とした円形に広がりながら伝搬していく。なおここでは、光が開口を通過しただけであるので波長は変化しない。
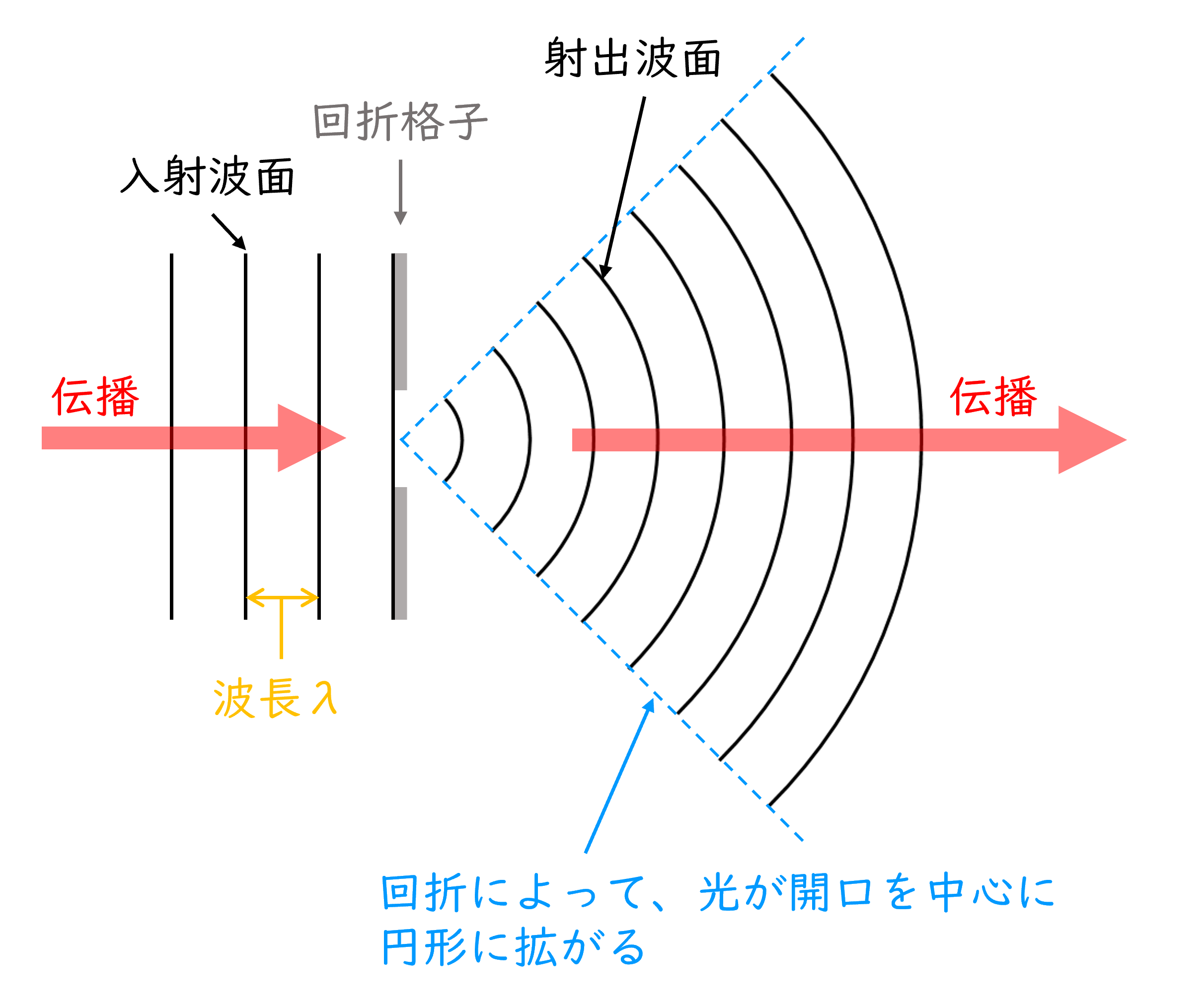
図2:古典的な回折格子の1 つの開口の拡大図。光は開口を通過後に回折によって開口の位置を中心とした円形に広がる。開口の通過前後で波長は変化しない。
それでは、図2のような開口が多数連なっている場合に考えを拡張していこう。回折格子の各開口を通過した光の波面が重なり合うと、各開口で回折した全ての光の波面を足し合わせた波面が形成されることになる。波面の足し合わせのことを「干渉」というが、まずは簡単のために2つの波面が重なった場合を考えよう(図3)。もし2つの波面の位置が揃った場合(波の山と山が同じ位置にきた場合)、それらの波を重ね合わせると強め合い、光の強度が強くなる(「強め合う干渉」という)。このとき波面の位置は元々の波面位置から変化しない。一方で、2つの波面の位置が互い違いになった場合(波の山と谷とが同じ位置にきた場合)、それらの波を重ね合わせると弱め合う(「弱め合う干渉」という)。このとき仮に元の2つの光の強度が全く同じであった場合は、波がちょうど打ち消しあって消えてしまうため、波面も消滅する(図3右)。
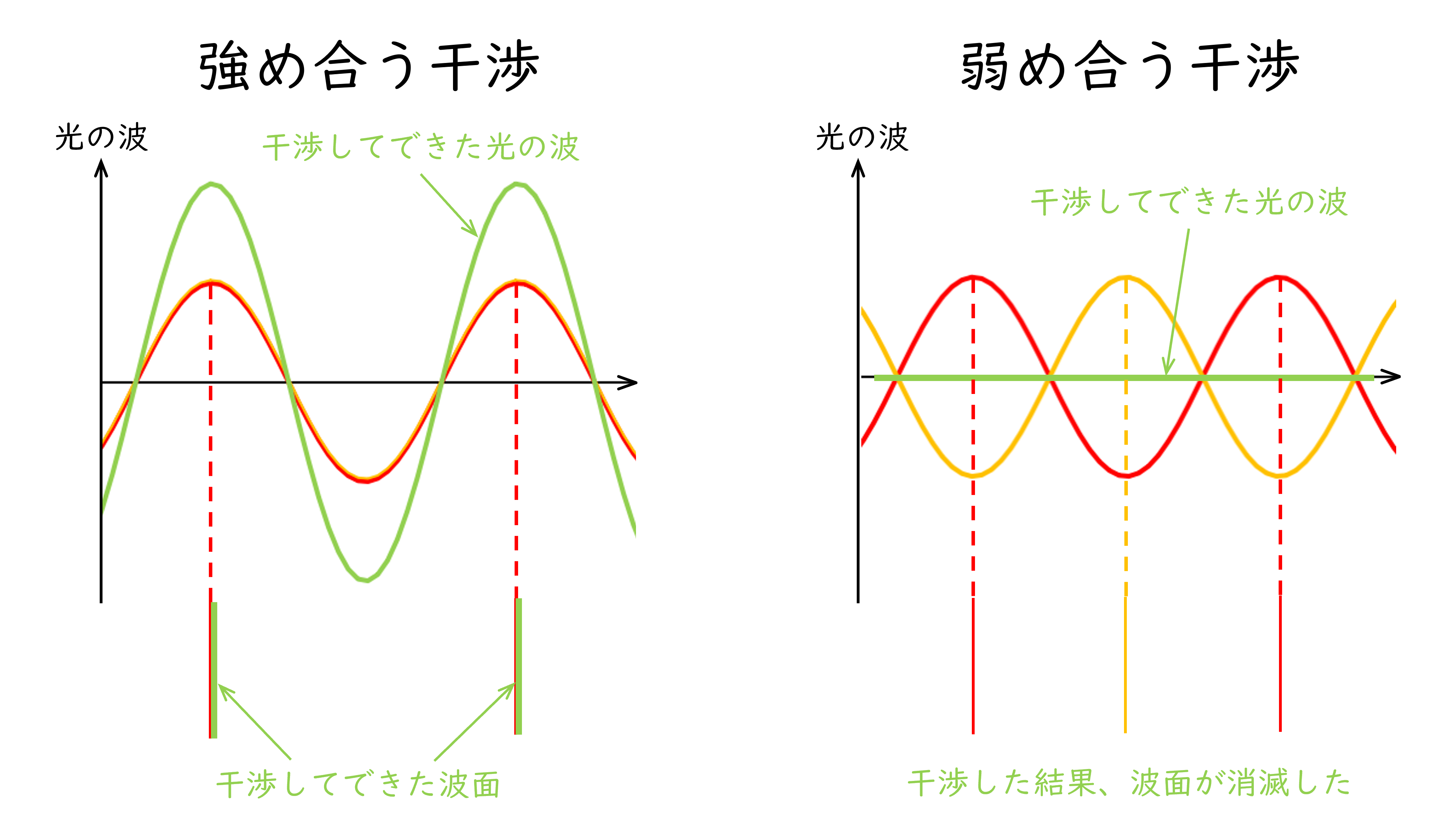
図3:光の干渉の模式図。強め合う干渉(左)と弱め合う干渉(右)をそれぞれ示した。
では、全ての開口からの波面が干渉した結果、最終的に回折格子はどのような波面を形成するのだろうか?この続きは次回に説明する。

大学院在学中は素粒子物理学を専攻。趣味の天体写真も物理理論に裏付けられた解析方法を行っており、 アマチュア天文家の間で蔓延している都市伝説は一切信じない。赤道儀マニアでアマチュア天文機器にやたら詳しい。 計算機ホログラム(CGH)や干渉計などの高度な物理計算を軽々とこなす。 光学・物理学に関連する原理や数学的理解に関する記事を担当。