
一般的に光学系内のミラーを調整する場合、その調整自由度は3方向への並進(\(X,Y,Z\))と3軸まわりの回転(\(\theta_{X}, \theta_{Y}, \theta_{Z}\))の6自由度である。ただし平面ミラーの場合、面内でミラーが動く分には光学性能は変わらないので、例えばミラー面内に\(XY\)平面を、法線に\(Z\)軸をとった場合は、並進の2軸(\(X,Y\))と回転の1軸(\(\theta_{Z}\))を除いた3自由度(=6-3)のみが調整に必要な自由度になる。具体的には、面に垂直な方向の位置(\(Z\))と面の傾き(\(\theta_{X}, \theta_{Y}\))を調整すればよいということである。平面ミラーにおけるこの事実は直感的にも分かりやすいので、光学調整を行ったことがある技術者であれば、たいてい身に着けている知見であろう。では、「球面ミラーにおいて最低限必要な調整自由度はいくつですか?」と問われると、即座に正解を打ち返すことができる技術者は意外に少ないかもしれない(仮に正解にたどりつけたとしても、少し時間を要するかもしれない)。今回は、この点について考えてみたい。
先に答えを言ってしまおう。実は調整自由度は平面ミラーと同じ”3”である(「え?」と思った方は、本稿を最後まで読んでほしい)。図1中の黒線は、光軸をZ軸とした曲率半径Rの凹球面ミラーを表している。球面に対して法線を立て、それを光軸かつ\(Z\)軸としよう。\(Z\)軸周りの回転(\(\theta_{Z}\))は、球面が回転対称性をもっていることから調整軸から落としてよいことは直ちにわかる。次に\(X\)方向に並進が生じた場合、すなわち凹球面ミラーが理想的な場合に対して\(\Delta X\)だけ並進ずれ(ディセンター)を起こしている場合を考える。図1の黒丸(点\(O\))と青丸(点\(O’\))はそれぞれ、並進ずれがない場合と\(\Delta X\)の並進ずれを生じた場合のミラー面の球心位置である。ここで、偏心前後のミラー面が交わる点(=\(A\))を考える。対称性から考えて、光軸から\(A\)までの距離は\(\Delta X/2\)になる。今、点\(A\)を中心として偏心後のミラーを回転することを考える。\(A\)から\(O\)までの距離(\(AO\))と\(O’\)までの距離(\(AO’\))は同じ(\(AO=AO’=R\))なので、点\(A\)を中心に\(\Delta \theta\)だけ回転させることで、\(O\)と\(O’\)を一致させることができることがわかる。球の中心と半径が一致しているということは、2つの面が完全に一致していることになる。つまり、「並進ずれの効果を回転によって完全に打ち消すことができる」ということである。
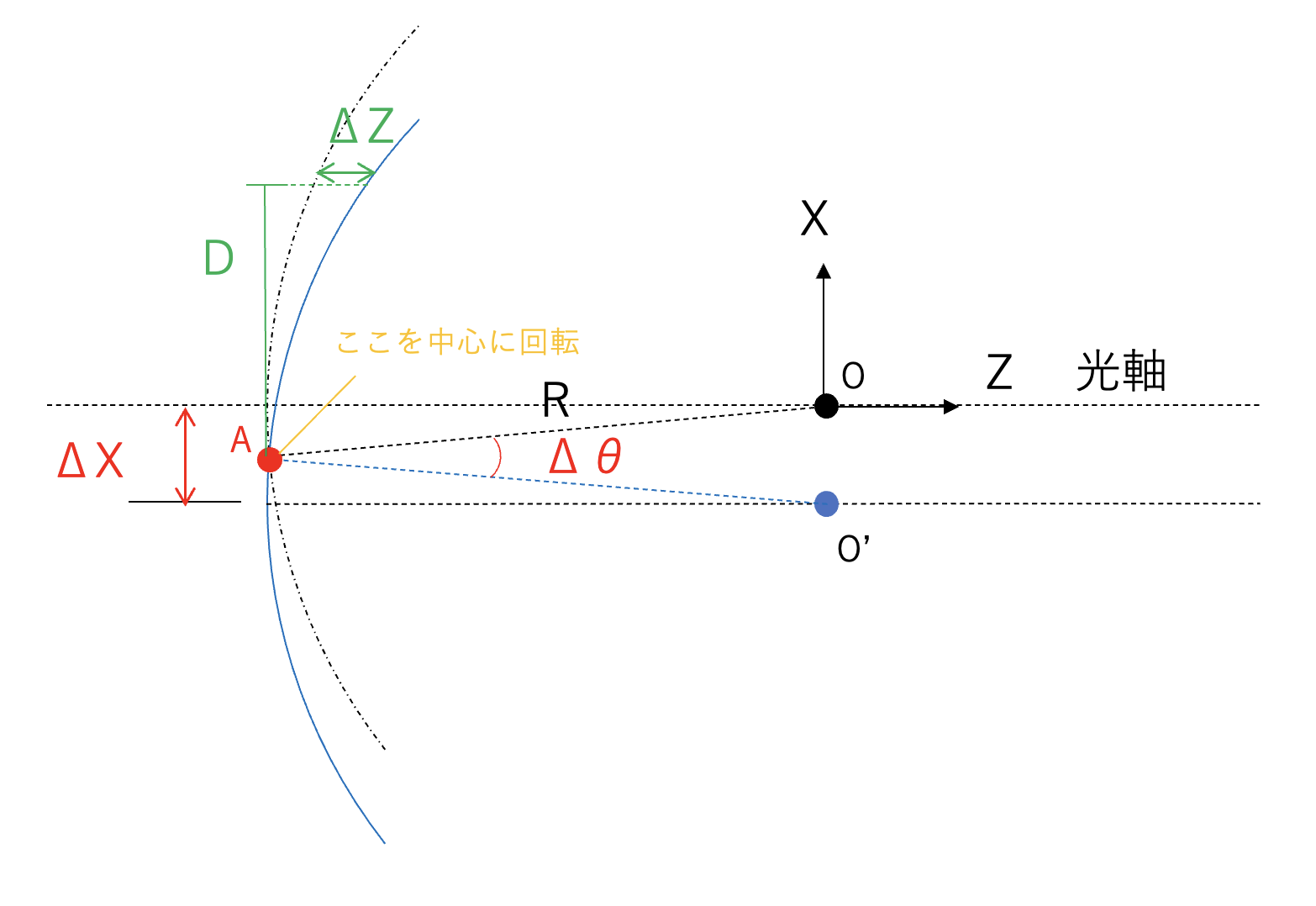
図1:光軸をZ軸とした凹球面ミラー(黒)が\(\Delta X\)だけディセンターした場合(青)
このことは、実際の光学調整においては並進か回転のどちらかの調整自由度は落としてもよいということを意味する。つまり、球面ミラーを調整する場合の最低限必要な自由度は、面に垂直な方向の位置(\(Z\))に加えて面の並進(\(X,Y\))もしくは、回転(\(\theta_{X}, \theta_{Y}\))の3(=1+2)自由度ということである。この知識は光学系の組立・調整を行う技術者だけでなく、オプトメカの設計者にとっても必須の知識である。より安定した光学系を実現するためには、光学系に設ける調整機構は可能な限り減らす、というのがセオリーだからである。
最後に並進量\(\Delta X\)とそれと同等な回転量\(\Delta \theta\)の関係を求めておく。図1の三角形\(AOO’\)の幾何関係から、
$$ R \sin\frac{\Delta \theta}{2} = \frac{\Delta X}{2} $$
という関係式が容易に得られる。調整の現場においては、一般に\(\Delta \theta \ll 1\)なので、\(\sin \frac{\Delta \theta}{2} \sim \frac{\Delta \theta}{2}\)と近似することで結局\(\Delta \theta \sim \frac{\Delta X}{R}\)となる。ミラーのサイズを\(D\)、回転に伴う調整量を\(\Delta Z\)とすると、\(\Delta \theta \sim \frac{\Delta Z}{D} \sim \frac{\Delta X}{R}\)が得られるが、多くのアプリケーションにおいては\(D < R\)であるため、一般的には\(\Delta Z < \Delta X\)になる。つまり、同じ角度調整\(\Delta \theta\)を行うのであれば、\(\Delta Z\)よりも\(\Delta X\)の方が大きいため、球面ミラーにおいては並進(偏心)調整(\(\Delta X\))の方が感度が鈍く細かい調整が行いやすいということになる(図1)。機構設計を行う上では、(回転調整機構よりも)並進(偏心)調整機構を設けた方がより精度の高い調整が可能になる。
さらに気になる読者は、双曲面や高次非球面などの回転対称面の調整に必要な自由度、さらには完全な自由曲面の調整に必要な自由度も考えてみてほしい。答えのみではあるが、それぞれ5と6となる。この解説はまた別の機会に。

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。