
光学用語として定義されている「倍率」には様々なものがある。最も有名なのは横倍率(\(\beta\))だろう。横倍率は物体と像のサイズ間の比として定義されるもので、直感的にも分かりやすい。わざわざ”横”倍率という名前がついているところからもなんとなく想像がつくが、実は”縦”倍率というのも存在する。今回はこの縦倍率について解説しよう。
横倍率で使う物体や像のサイズは光軸に対して”垂直”な方向の長さのことである。長さyの棒(線分)を光軸に対して垂直に置いたとき、得られる像も長さy’も光軸に対して垂直になるが、yとy‘の比(=y’/y)が横倍率である。では、光軸に対して長さzの物体を光軸に対して平行に置いた場合はどうだろう?近軸光学の理論によると、光軸にある点から発せられたすべての光は光学系(レンズ系)通過後、光軸上の別の点に再び集まるという性質(アッベの不変量)がある。したがって、光軸に沿った長さzの物体に対しても、それに相当する軸に沿った長さz’の像が得られることになる。光学系(レンズ系)は、光軸に垂直な面のみならず奥行方向に対しても像を生成できるのである。このとき、zとz’の比(=z’/z)を縦倍率といい、ギリシャ文字の(\(\alpha\))で表すことが多い。
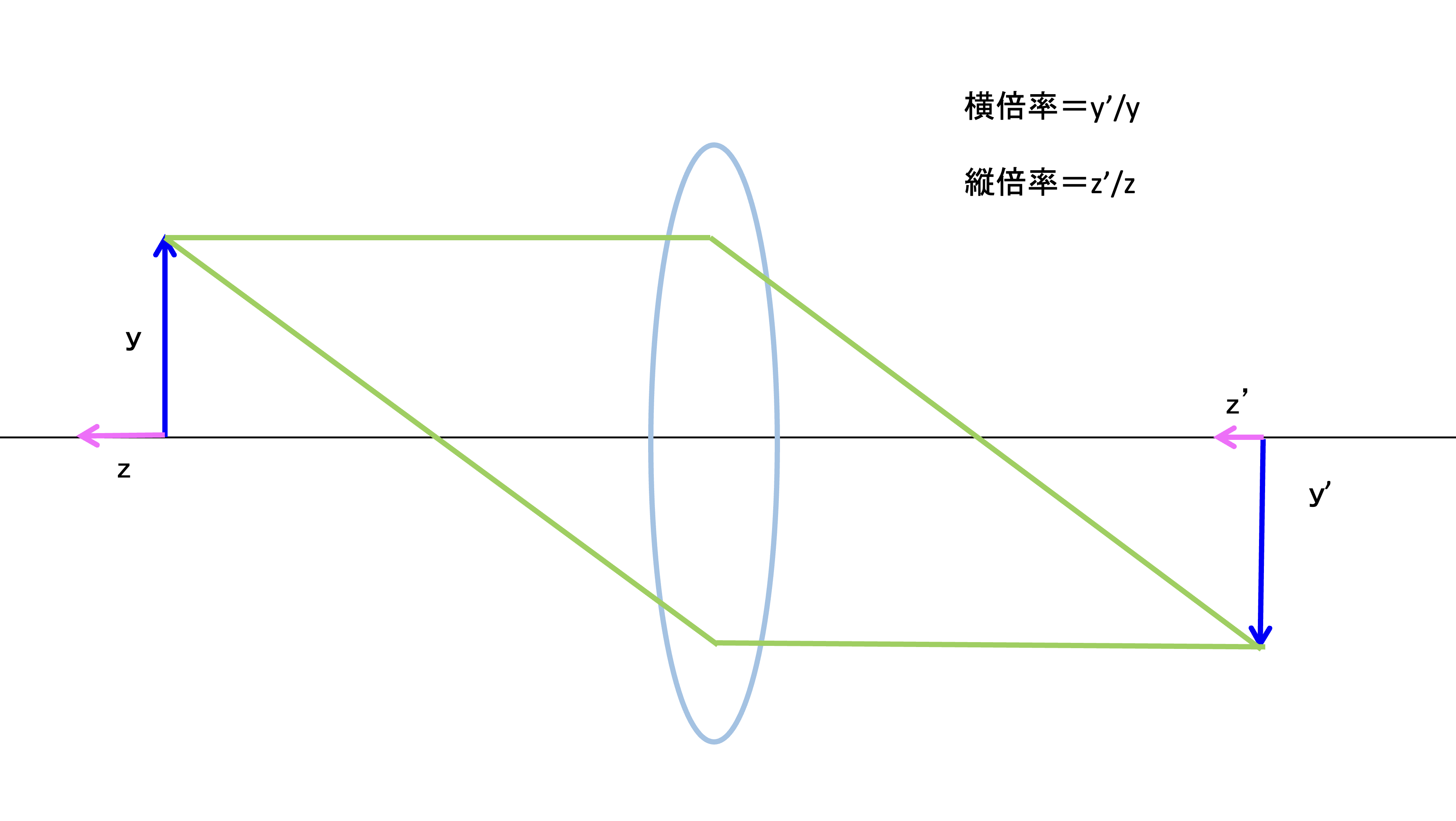
図1:横倍率と縦倍率
定義が分かったところで、縦倍率の性質を実際に数式を用いて調べてみよう。導出には毎度おなじみレンズの公式を用いる。
$$\frac{1}{a} + \frac{1}{b} = \frac{1}{f}$$
ここで、aとbはそれぞれ物体および像から主平面までの距離である。今、aとbを光軸に沿っておいた棒の一端までの距離とすると、もう一方の端に対しては同じくレンズの公式を用いて以下の式が成り立つことが分かる。
$$\frac{1}{a+z} + \frac{1}{b-z’} = \frac{1}{f}$$
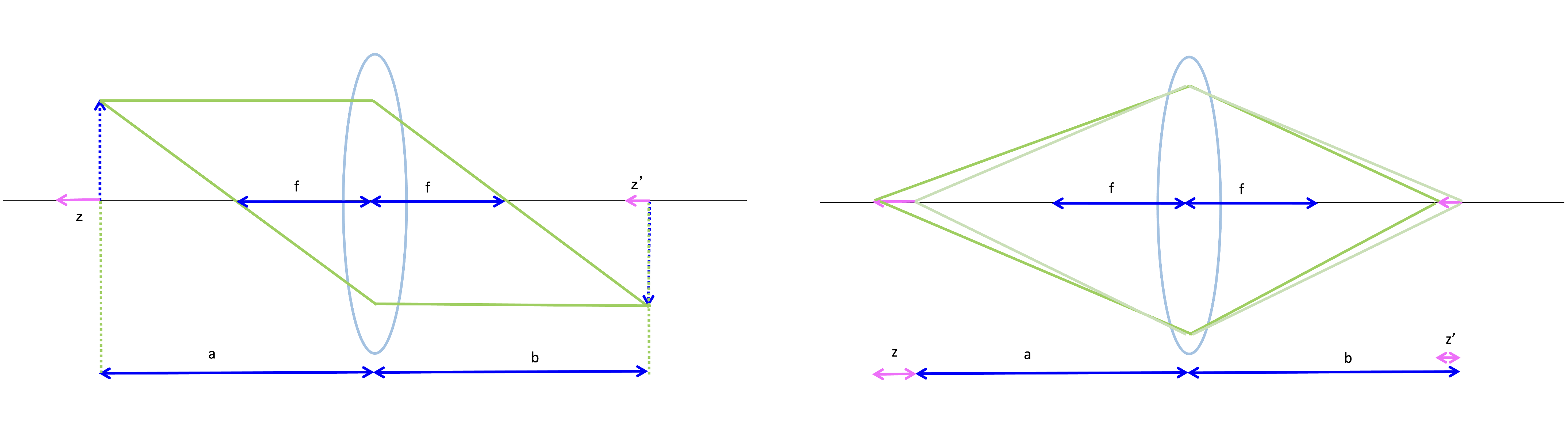
図2:縦倍率と横倍率とレンズの公式
先の2式を連立させると、
$$\frac{1}{a} – \frac{1}{a}\frac{1}{1+\frac{z}{a}} = \frac{1}{b}\frac{1}{1+\frac{z’}{b}} – \frac{1}{b}$$
となる。ここで、一般に棒の長さがレンズまでの距離よりも小さい(zとz’はaとbに対して十分小さい、z/a, z’/b << 1)とすると、\(\frac{1}{1+\frac{x}{a}} \sim 1-\frac{x}{a}\) の関係と横倍率\(\beta(=\frac{y'}{y})\)が物体距離と像距離の比(\(=\frac{b}{a}\))で表せることを用いると、 $$\alpha = \frac{z'}{z} = \left(\frac{b}{a}\right)^2 = \beta^2$$ が得られる。縦倍率は横倍率の二乗になるのである。深く考えない範囲においては、縦倍率は横倍率に比例しそうな気がするが、そうは問屋が卸さないというのが、ここで重要な点である。
縦倍率の性質を使った例として焦点深度と被写界深度の関係がある。焦点深度\(\Delta^{\prime}\)は優位なピンボケが発生していない結像点の許容範囲であるが、それを光軸に沿った長さ\(\Delta^{\prime}\)の仮想的な像であるとも考えることができる。その時、それに対応する仮想的な物体サイズ\(\Delta\)は被写界深度に相当し、その長さは\(\Delta=\frac{\Delta^{\prime}}{\beta^{2}}\)となる(\(\beta\)は横倍率)。たとえば、CCDカメラを用いて横倍率200倍の顕微光学系を構築したとする。一般に顕微鏡レンズは、非常に明るい光学系であるため、被写界深度が非常に浅い。仮に被写界深度が\(\Delta = 0.1\mu m\)の場合、像側(CCDカメラ側)の焦点深度は\(\Delta^{\prime} = 0.1\mu m \times 200^2 = 4mm\)となり、物体側の光軸方向のわずかなずれに対して、大きな梃子を効かせることができる(=CCD側でそれほど厳密な焦点合わせをすることなく、物体側の細かい奥行情報を得ることができる)。顕微鏡とは、物体と像が逆の関係になっているのが望遠鏡である。宇宙には無数の天体が望遠鏡の光軸方向に沿って、数光年~数億光年のとてつもなく大きな距離範囲に広がっているが、とてつもなく大きな天体を小さなCCDやCMOSなどに結像できるほど小さな瞳倍率(\(\beta \ll 1\))であるため、異なる距離にある天体間でピンボケを生じることなく、すべての天体の像はほぼ同じ平面に合焦できるのである。

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。