虹を理解する　その２

ただこれだけでは光が水滴の中を通って虹色に分かれる理由になっていない。光が虹色に分かれるのは、水滴内を進む光の速度（つまり屈折角）が色ごとに異なるためである。

光は波の性質を持つが、波の１周期の長さ（波長）の違いが人間には色の違いとして認識される。目で見える光の波長はおよそ380〜700nm程度であり、波長が短いほど青く、長いほど赤く見える。屈折は媒質中を進む光の速度が異なることで、異なる媒質の界面で光が曲がる現象だが、この屈折角（つまりは屈折率）が波長によって異なっている。目で見える波長（可視光域）の場合には青い光ほど屈折率が大きく（光の屈折度合いが強く）、赤い光ほど屈折率が小さい（光の屈折度合いが弱い）ことがわかっている。

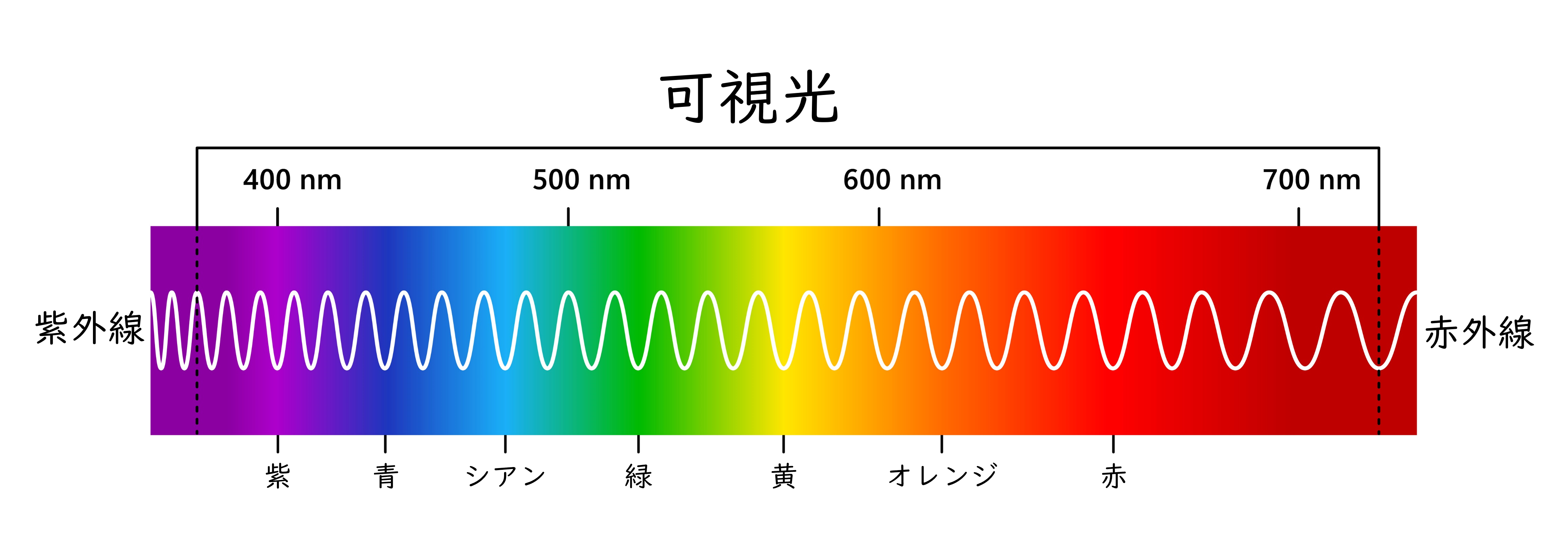
図１：目で見える光（可視光線）の波長

この屈折率の波長依存性のことを専門的には「分散」と言うが、分散についての説明は別の機会に譲ることにする。ここでは端的に、屈折率と波長の関係を示した経験式のうち、よく使われているものを紹介しよう。ドイツの理論物理学者のウォルフガング・セルマイヤーが1870年代に波長（\(\lambda\)）と屈折率（\(n(\lambda)\)）の関係を表す経験式（セルマイヤーの式）を提案した。

$$ n^{2}(\lambda)=1+\sum_{i}\frac{B_{i}\lambda^{2}}{\lambda^{2}-C_{i}}　$$

B_i、C_iは物質によって決まる定数である。なお光学ガラスとしてよく利用されるBK7のi=3までのB_i、C_iは以下の値が与えられている。

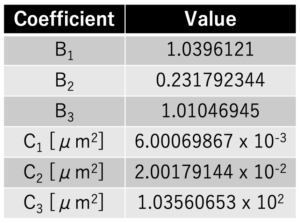
表1：BK7におけるセルマイヤーの経験式の係数B、Cの値(i=3)

なおこの分散を示す式はセルマイヤーの経験式以外にも複数存在しているが、セルマイヤーの経験式は分散理論から得られる理論式とも整合している。セルマイヤーの経験式から、\(\lambda\)の値が大きいほど、屈折率nが小さい値をとることがわかる。

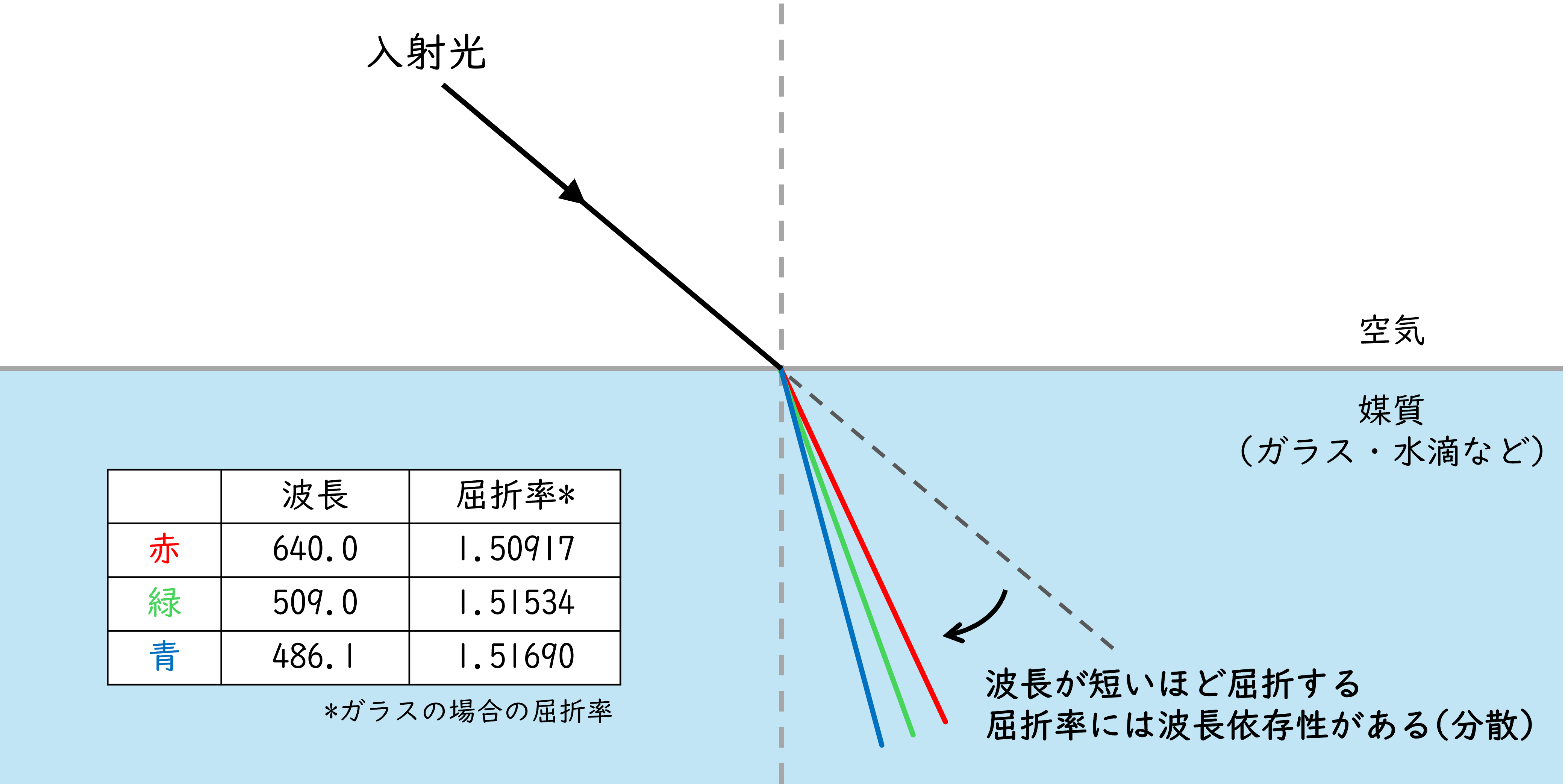
図２：波長による屈折率の違い（分散）模式図

c

まとめると、水滴に入射した太陽光が、この分散の効果によって波長ごとに水滴内を進む光路が変化し、その結果光が色ごとに別れて水滴から出てくるようになるのだ。しかし勘の良い読者の方はこう思ったかもしれない。「あれ？これだけでは、どんな方向にも虹が放出されるはずでは？」と。。。そう、この効果だけではいつ、どこでも虹が見えるわけではないこと、ひいては円環状に見える理由にもなっていないのだ。

次回は、水滴の中を進む光を具体的にシミュレーションし、虹が見える条件が限られている理由と、円環状に見える理由について紹介しよう。