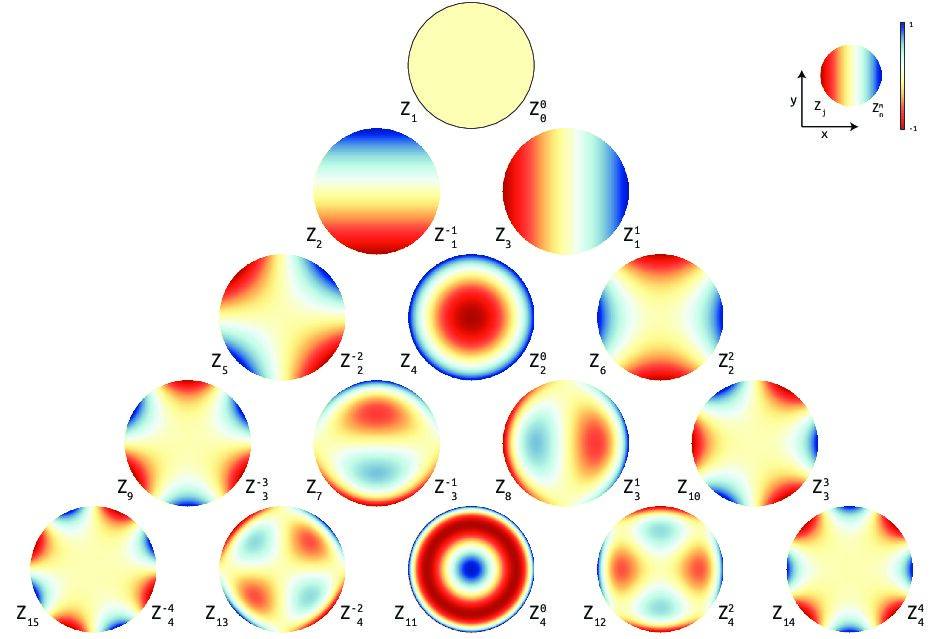
光学において、波面(誤差マップ)の中にどの収差成分が含まれているのかを判別するのにしばしば使われるZernike多項式。今回はこの多項式の項の意味について考えてみたい。
Zernike多項式にはいろんな流儀があるが 、多くの干渉計に実装されているFringe Zernike多項式の場合、第1項はピストン(位相のゼロ点シフト)、第2項と第3項は波面の傾き(ティルト)、第4項はデフォーカスを示すと教えられる。これらは近軸量であり、結像面に置かれた検出器のシフトとフォーカス調整によって補償が可能なため、現場の波面測定においてはそれらの項の寄与を差し引いて評価されることがしばしばである。
実際、第1項と第2・3項は\(Z_{0}(x,y)=1\)、\(Z_{1}(x,y)=x\)、\(Z_{2}(x,y)=y\)であり、波面の絶対位相と傾きを表していることが直ちに理解できる。ところが、第4項を確認すると\(Z_{4}(x,y)=2(x^{2}+y^{2})-1\)となっているではないか(!?)。フォーカスで調整可能であれば球面の式になっているはずであるが、これは放物面の式である。言われてみれば確かにそうなのであるが、Fringe Zerike多項式の第4項(一般にZernike多項式の”パワー項”と言われる項)は、厳密にはデフォーカスを表していないのだ。
放物面は、光線追跡ソフトウェアにおける表現を使うと、曲率半径がR、円錐(コーニック)係数がk=-1である。一方、球面の場合は曲率半径がR、円錐係数はk=0であるので、これら両方の形状は近軸理論の範囲においては一致する。波面誤差を評価する場合は、Rは有効径に対して十分大きいことが通常であるので、放物面と球面の差はごくわずかになる。これがおそらく、放物面の項をデフォーカス項と呼ぶ理由であろう(あくまで筆者推測による)。となると、その差が大きくなり「デフォーカス項」と呼んではいけない範囲が存在するはずである。それについて調べてみた。
図1は、横軸にF値を、縦軸に曲率半径Rをとったときの放物面の理想球面に対する波面誤差の最大値(PV値)をマッピングしたものである。ここでのF値は測定対象のビーム径をDとしたとき、F=R/Dとして定義している。よってFが小さくなるほど(Dが大きくなるほど)波面誤差が大きくなるはずである。波面誤差は\([\mu m]\)の単位で示している。Zernike多項式のパワー項をでフォーカス項として近似した場合の波面誤差が1\(\mu m\)(PV)になるためには、光束がF/3の場合はR=10mm以下、 F/10の場合はR=1,000mm以下、F/30の場合は、R=10,000mm以下である必要があることが分かる。集光光束もしくは発散光束を評価する場合は意外に誤差が大きく、Zernikeのパワー項をデフォーカス量と盲目的に信じるのは危険である、という結果である。
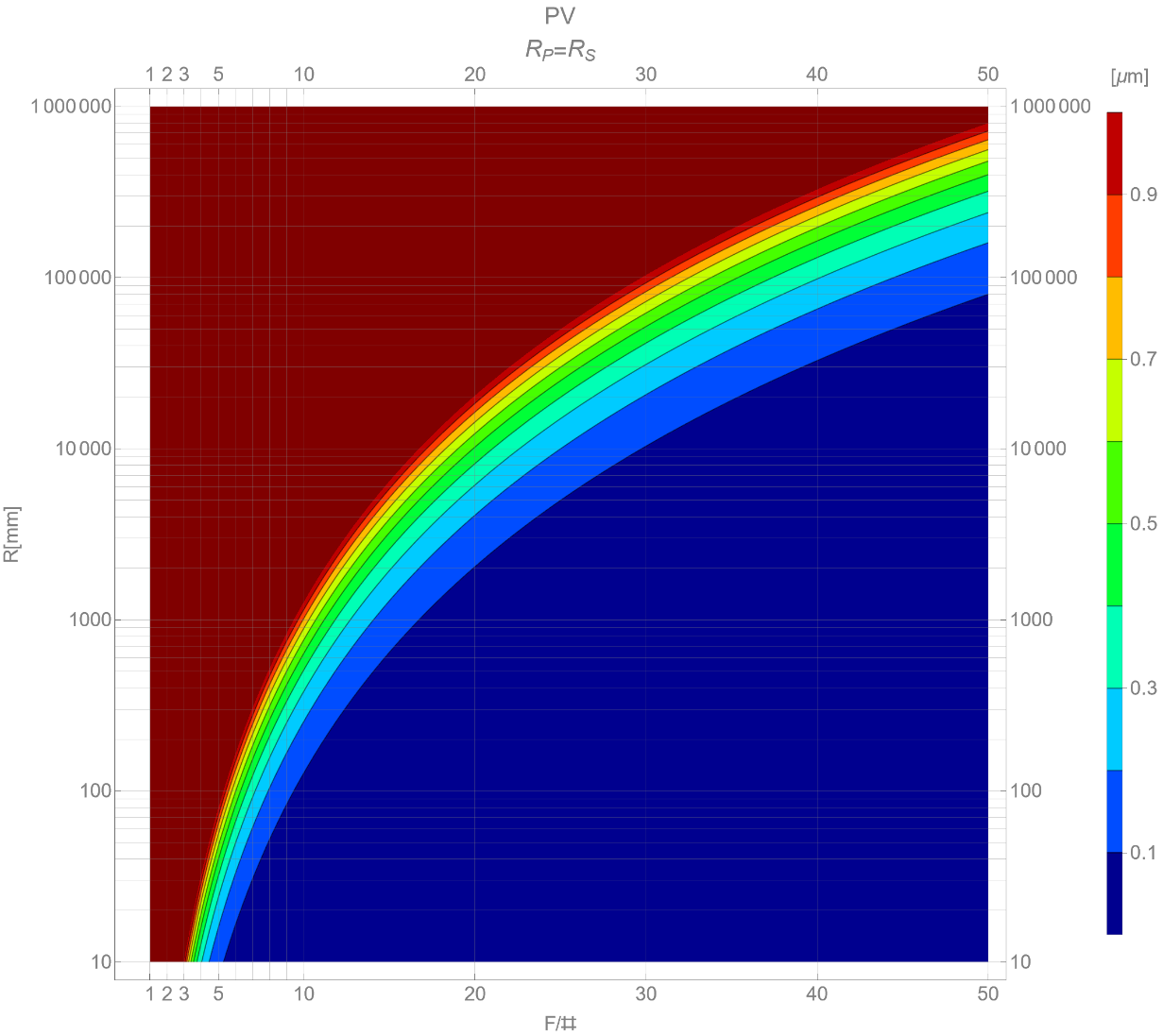
図1:Zernikeパワー項(Fringe Zernike第4項)の理想球面(R)に対する波面誤差のPV値。横軸はF値、縦軸は理想球面の曲率半径。
そこで、今度は放物面を適当な曲率半径(R’)を用いて近似し、得られた近似球面と放物面の差分(の最大値)を示したのが図2である。このとき、放物面を近似する曲率半径はもはやRではないが、測定の現場においては(頂点曲率半径を知る術がないため)より現実に近いと考えられる。この場合は、より広い範囲で誤差は小さくなる。例えば、図1と同じ条件を設定すると、評価する光束がF/3の場合はR=40mm以下、 F/10の場合はR=5,000mm以下、F/30の場合は、R=40,000mm以下での範囲でパワー項を以てデフォーカスと呼んでよいことが分かる。なお、図2を得るための曲率半径R’は、放物面と近似球面の差のPV(Peak-to-Valley)が最小となるように選んでおり、\(\Delta R=R’-R=R/(16F^{2})\)の関係になることが詳細な計算から得られる。読者の中には、「RMSを最小にする場合はΔRのどうなるの?」と鋭い質問をされる方もおられる方もいるかもしれない。でもそこは安心してほしい。RMS値を最小になるようにR’を決めた場合でも、同じ結果(\(\Delta R=R/(16F^{2})\))になる。実に面白い。。。
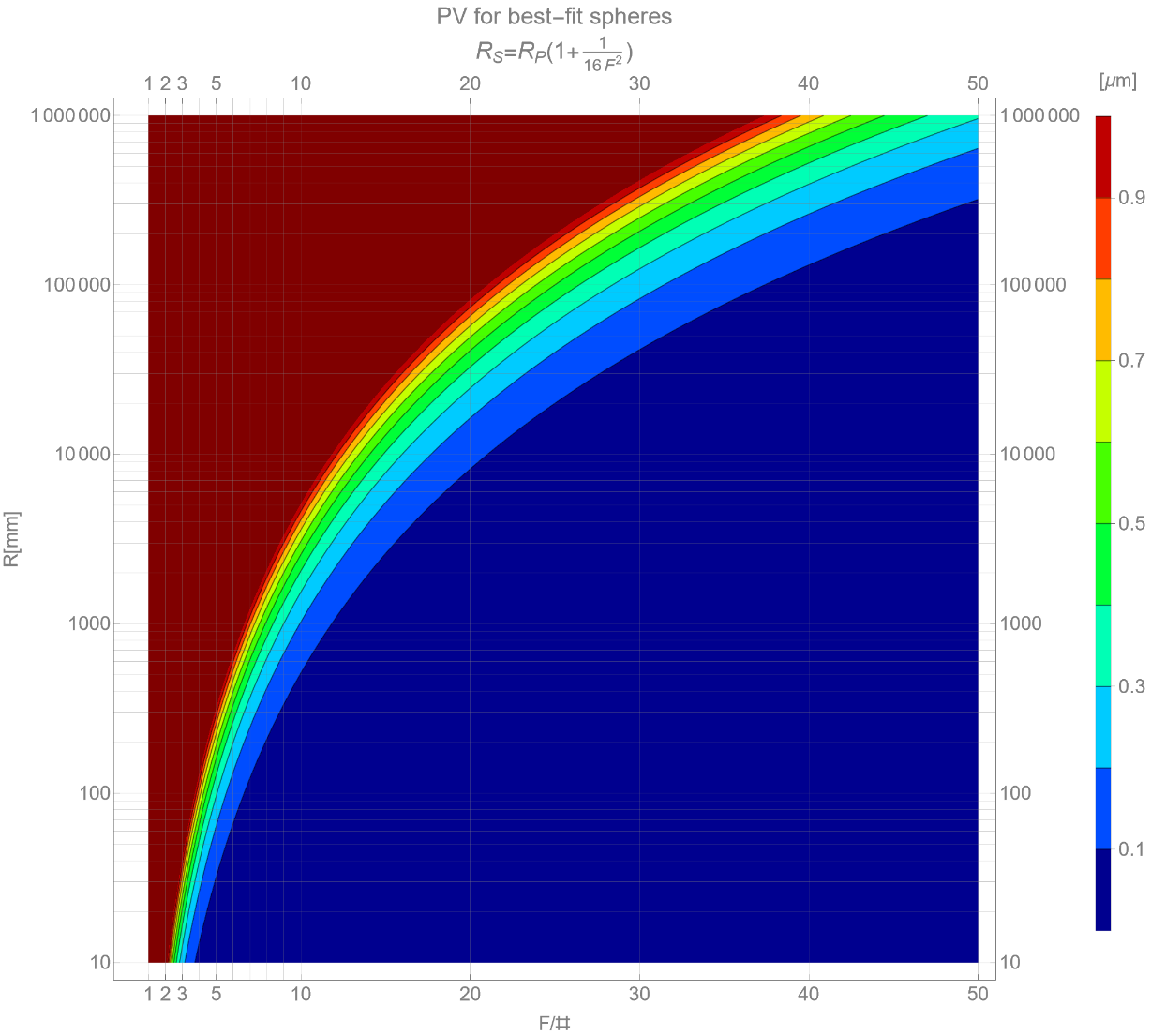
図2:Zernikeパワー項(Fringe Zernike第4項)の近似球面(R’)に対する波面誤差のPV値。横軸はF値、縦軸は理想球面の曲率半径。

大学院在学中に自らが計画して手掛けた偏光分光装置の開発がきっかけで光学に魅了される。 卒業後民間光学会社に就職し、2006年にフォトコーディングを独立開業。 官民問わずに高品質の光学サービスを提供し続ける傍ら、2009年より京都産業大学にも籍を置き、 天文学と光学技術を次世代に担う学生に日々教えている。 光学技術者がぶつかるであろう疑問に対するアンサー記事を主に担当。