波面収差の定量化：波面収差の定義とその定式化（１）

前回の記事では、理想結像に対する波面が球面波であることを説明したが、そもそも収差を持った光学系から射出される波面はどうなるだろうか。この場合の波面における収差は、幾何光学的な収差を「理想結像点からのずれ」と考えたのと同じように考えることができる。具体的には理想波面（＝球面波）からのずれと考えることができ、これを「波面収差」とよぶ。

より厳密な波面収差の定義は次の通りである。まず、理想球面波の中心(＝理想結像点）とその理想球面波が空間内のどこにあるかを決める「理想球面波の半径」が必要である。理想結像点は、近軸像点の位置として定める(図１)。理想球面波の半径は、射出瞳に頂点を持つ球面を考えることで定まる。詳細は別の記事に譲るが、射出瞳とは光学系を像側からのぞいた場合の絞りの像面であり、そこではすべての視野からの主光線が(理想的には)１点に重なる（図２）。こうして定義された理想球面波は「ガウスの参照波面」とも呼ばれる。そして、実際の波面と理想球面波との”ずれ”を理想球面波に直交する光線に沿って測ったものが「波面収差」である（図１）。

 

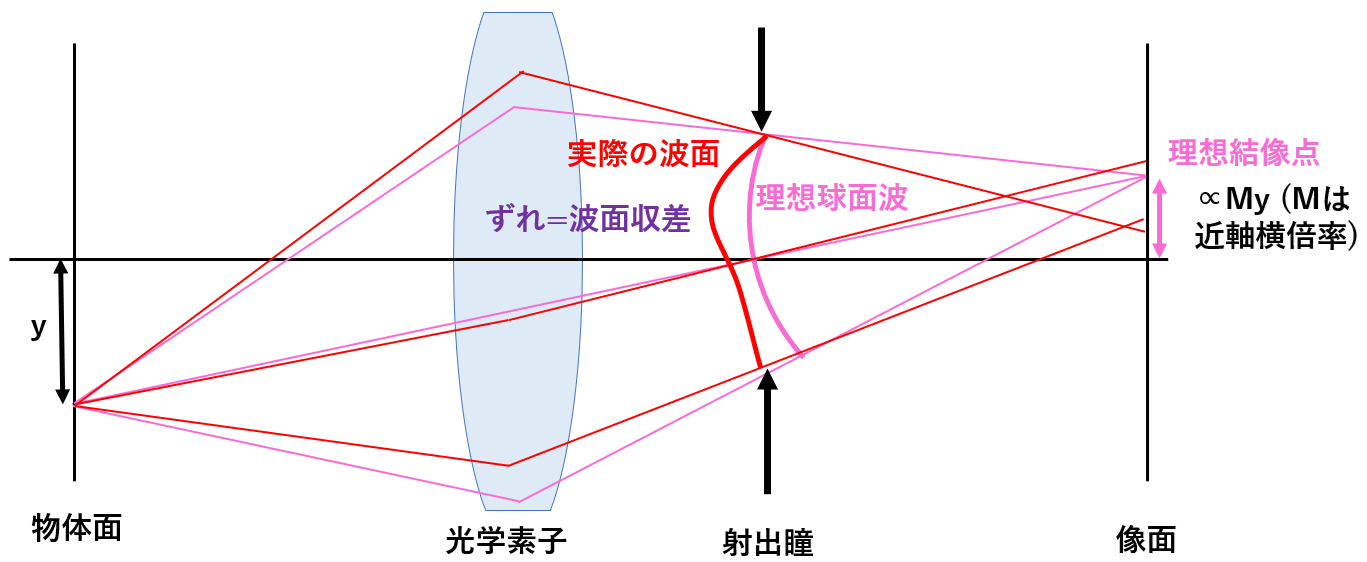
図１：波面収差の概要

 

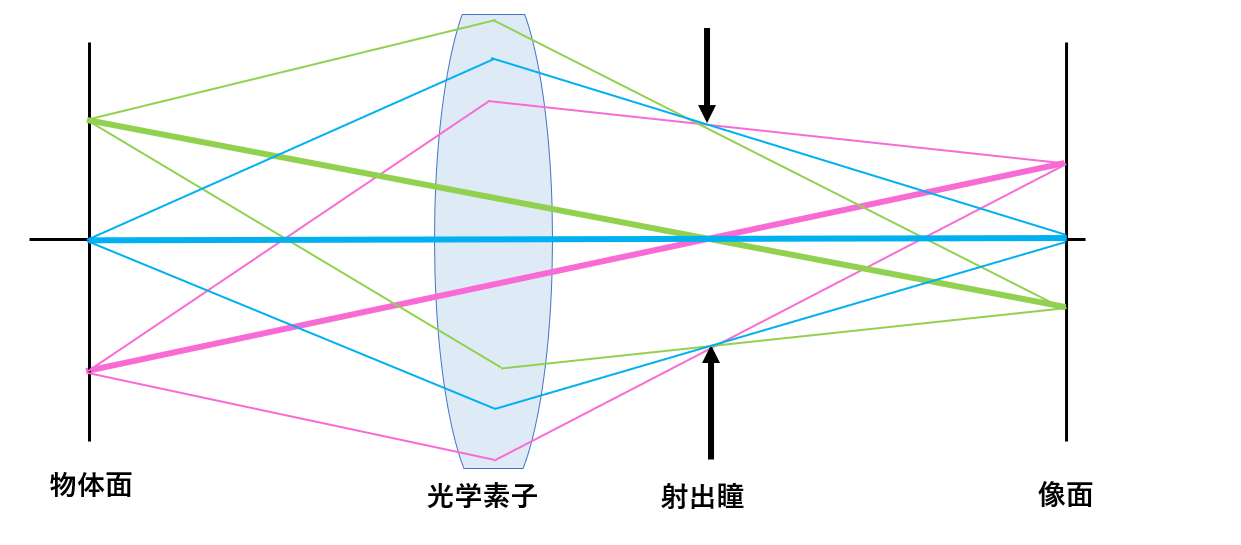
図２：射出瞳の説明図：各視野からの光線束のうち、主光線のみを太線にしてある。
射出瞳上ではすべての画角からの主光線は一点で交わる。

 

波面収差は射出瞳上の位置によって異なる。また、波面収差は幾何学的収差と同様に各視野ごとにも異なる。つまり、射出瞳面上（もしくは入射瞳面上）に置かれた座標\((\rho_x, \rho_y)=\vec{\rho}\)と視野の位置(すなわち、像面での結像点の位置)\((H_x, H_y)=\vec{H}\)との関数になるため、波面収差\(W\)は\(W=W(\vec{\rho}, \vec{H})\)と書くことができる。(なお、慣例的に最大視野と瞳半径は1とすることが多い。)\(W(\vec{\rho}, \vec{H})\)を特に、「波面収差関数」と呼ぶことがある。波面収差関数は原理的には\(1,\vec{\rho},\vec{H},\vec{\rho}\cdot\vec{\rho},\vec{\rho}\cdot\vec{H},\vec{H}\cdot\vec{H},\vec{\rho}\times\vec{H},…\)といった\(\vec{\rho}\)と\(\vec{H}\)を使って表現されるあらゆる項からなる多項式として展開できるが、光学系が回転対称性と(光軸を含んだ)平面対称性の両方を持つ場合は、その展開式は\((\vec{\rho} \cdot \vec{\rho}), (\vec{H} \cdot \vec{H}), (\vec{H} \cdot \vec{\rho})\)とそれらの組み合わせのみが現れた以下の形式で書ける。

\begin{align}
W(\vec{\rho}, \vec{H}) =\
& W_{000} + W_{020}(\vec{\rho} \cdot \vec{\rho}) + W_{111}(\vec{H} \cdot \vec{\rho}) + W_{200}(\vec{H} \cdot \vec{H}) \notag \\
& + W_{040}(\vec{\rho} \cdot \vec{\rho})^2 + W_{131}(\vec{H} \cdot \vec{\rho})(\vec{\rho} \cdot \vec{\rho}) + W_{220}(\vec{H} \cdot \vec{H})(\vec{\rho} \cdot \vec{\rho})　\notag \\
& + W_{222}(\vec{H} \cdot \vec{\rho})^2 + W_{311}(\vec{H} \cdot \vec{H})(\vec{H} \cdot \vec{\rho}) \notag \\
& + W_{400}(\vec{H} \cdot \vec{H})^2 + \cdots
\end{align}

ここで\(W_{ijk}\)は波面収差関数の各展開項の係数であり、\(i,j,k\)はそれぞれ各展開項が有する\(\vec{H}, \vec{\rho}, (\vec{H} \cdot \vec{\rho})\)の次数を表す（\(\vec{H} \cdot \vec{\rho}\)は\(\vec{H}\)と\(\vec{\rho}\)のなす角\(\Delta \theta\)を用いて\(cos\Delta \theta\)と書かれることもある）。例えば、\(W_{131}(\vec{H} \cdot \vec{\rho})(\vec{\rho} \cdot \vec{\rho})\)であれば、\(\vec{H}\)が1つ、\(\vec{\rho}\)が3つ、\(\vec{H}\cdot\vec{\rho}\)が1つ含まれるので、その係数が\(W_{131}\)となる。この展開式において\(n=i+j\)をその項の”次数”と呼び、特に４次の各項はザイデル収差のそれぞれに対応する。その話は別の記事にて述べることにして、次回はより低次の０次、２次の項を詳細に見てみよう。