波動光学的に考える焦点深度　その２

図１は前回の記事で扱った図３と同じものであり、光学系に焦点ずれが発生した場合の波面収差の説明図である。光軸上の結像点\(I\)と光軸から高さhの距離にある射出瞳上の点\(R\)を結ぶ直線を描き、それが\(I’\)に理想結像する波面と交わる点を\(R’\)とする。点\(I’\)に検出器を置いた場合は、実際の波面は点\(I\)に理想的に集光するため、理想結像に対して線分「\(RR’\)だけ光路差を持った状態」ということになるが、この線分\(\overline{RR’}\)の長さを「波面収差」と呼ぶのであった。

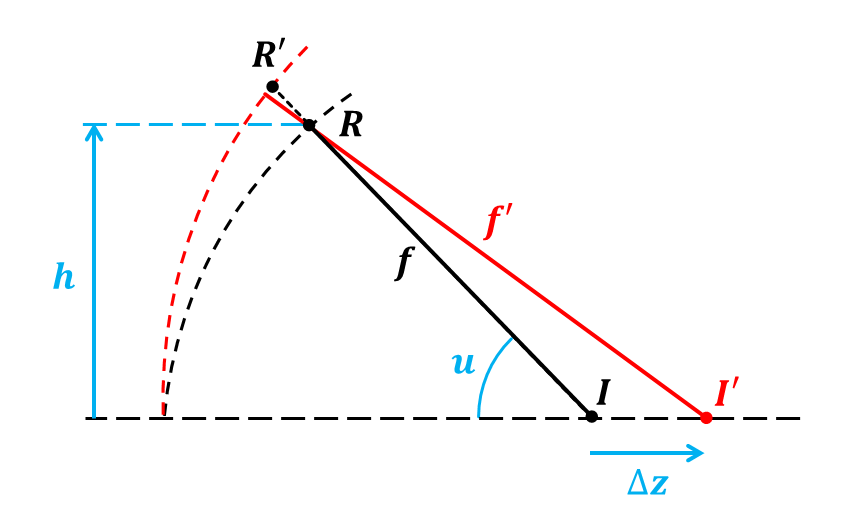
図１：デフォーカスの場合の波面収差

 

この状況に対して具体的に波面収差\(\overline{RR’}\)を求めてみる。図より、\(f’ = \overline{RR’} + f + \Delta z \cos{u}\)なので、

$$ RR’ \simeq (f’ – f) + \Delta z \cos{u} = \Delta Z_{\text{wfe}}(1-\cos{u}) \sim \Delta Z_{\text{wfe}} \frac{h^2}{2f^2} $$

であることが分かる。なお、ここでは\(\frac{h}{f} \ll 1\)として、2次の項までを採用している。

ここまで準備でようやく波動光学的な焦点深度を議論することができる。波動光学において像のボケが無視できる基準としてよく使われる量としてレーリー限界（Rayliegh limit）がある。これによると、最大波面収差が\(\frac{\lambda}{4}\)であれば画像は劣化していないとみなせる（なぜ\(\frac{\lambda}{4}\)なのかとういうことは紙面の都合上ここでは述べないが、改めて別稿に記載するので、ここでは「そういうものか」と受け入れていただきたい）。上式の波面収差（\(\overline{RR’}\)）がこのレーリー限界（\(\frac{\lambda}{4}\)）と一致するとすれば、

$$ \Delta Z_{\text{wfe}} \simeq (f’) = 2 \lambda F^2 $$

が得られる。ここでの式変形には\(F = \frac{f}{2h}\)を用いた。なんと、面白いことに幾何光学的な焦点深度はF値に比例する（前回の記事を参照）のに対して、波動光学的な焦点深度はF値の２乗に比例する（F値が大きくなると急激に大きくなる）のだ。これは回折の効果によってF値が小さくなる（大きくなる）ほど、点像サイズが小さくなる（大きくなる）ことが関係している。つまり、F値が大きくなると、それにつれて点像が大きくなるので、ボケが目立ちにくくなるからである。

幾何学的焦点深度\(\Delta Z_{\text{geo}}\)と波動光学的焦点深度\(\Delta Z_{\text{wfe}}\)を比較したのが図２である。図の横軸はF値、縦軸は各場合における焦点深度を示している。幾何学的焦点深度については\(\gamma=1\)とし、検出器のピクセルサイズが2\(\mu m\)（紫線）、5\(\mu m\)（緑線）、10\(\mu m\)（水色線）の場合を示している。また、波動光学的焦点深度（橙線）については、波長をλ=500\(nm\)（可視光）としている。図から、F値が小さいときは、”幾何学的焦点深度 > 波動光学的焦点深度”であり、光学系の評価にはより厳しい（小さい）値になる「波動光学的焦点深度の方を用いるべき」であることが分かる。反対に、F値が大きくなると”幾何学的焦点深度 < 波動光学的焦点深度"となり、波面収差の量よりもピントずれによる幾何学的な像のボケの方が影響が大きくなるので、「幾何学光学的焦点深度の方を用いるべき」ということになる。その境目となるF値は検出器のピクセルサイズが2\(\mu m\)の場合でF/2、5\(\mu m\)の場合でF/5、10\(\mu m\)の場合でF/10である。

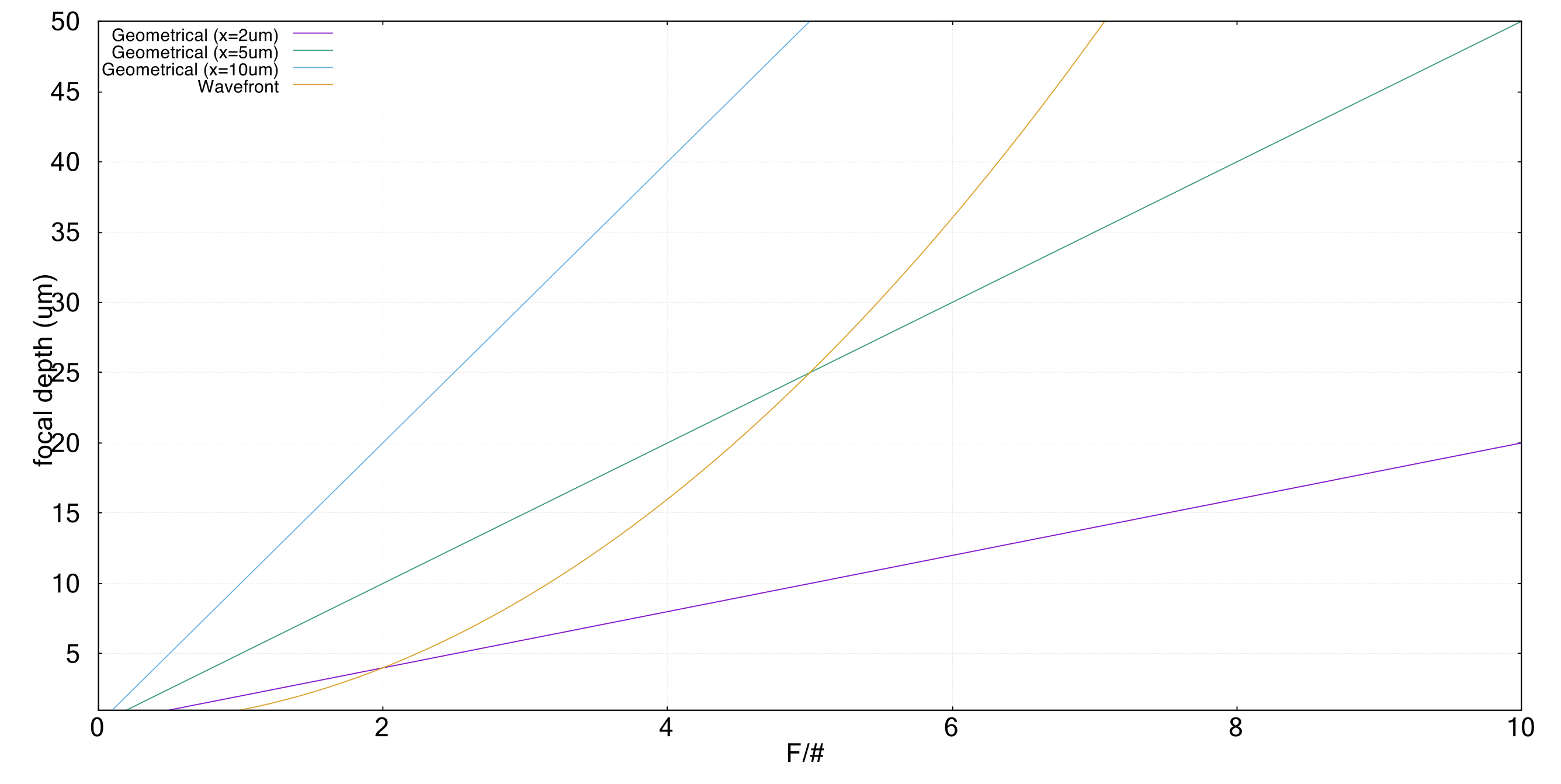
図２：幾何学的焦点深度と波動光学的焦点深度の比較

 

この波動光学的焦点深度は波面収差を使った量であるため、収差を持った光学系に対しても適用できる。次回は、そのような光学系に対して適用した場合について考察してみたい。